모델이 학습 데이터에 과적합되는 것을 방지하기 위해 규제를 적용한다.
선형 회귀의 목표는 오차가 최소화되는 모델을 만드는 것이다.
다만, 다중 선형 회귀 모델에서 오차가 작아지는 회귀 계수(W)들을 찾는 데만 집중하다보면,
간혹 모델이 과적합되어 회귀 계수 값이 너무 높게 산출되는 현상이 발생하기도 한다.
이러한 과적합 현상을 방지하기 위해 일반 선형 회귀 모델에 규제를 적용한 규제 모델을 사용한다.
이번 포스팅에서는 세 가지의 규제 선형 회귀 모델을 알아본다.
그 전에 회귀 모델의 적합도와 성능을 평가하는 결정계수(R²)와 손실함수를 살펴보려고 한다.
결정계수(Coefficient of Determination)
회귀 모델의 적합도는 결정계수(R², R-squared)를 통해 평가한다.
결정계수란 종속변수의 전체 변동성 중 회귀식이 설명할 수 있는 변동성의 비율을 말한다.
즉, 독립변수가 종속변수의 변동을 몇 퍼센트(%)나 설명하는지를 나타내는 지표이다.
결정계수(R²)는 다음과 같은 식을 따른다.

- SST(Total Sum of Squares, 전체제곱합) : 전체 변동
- SSR(Regression Sum of Squares, 회귀제곱합) : 회귀선으로 설명 가능한 변동
- SSE(Error Sum of Squares, 오차제곱합) : 회귀선으로 설명 불가능한 변동
* 결정계수는 0과 1 사이의 값을 가지며, 1(100% 설명)에 가까울수록 모델의 적합도가 높다.
결정계수를 구성하는 변동성 값들을 좀 더 살펴보자.
실제값(y)이 회귀선과 가까운 정도를 실제값(종속변수)의 변동성(분산)을 이용해 측정할 수 있다.
분산은 실제값과 평균의 차이를 의미한다.

그림에서 빨간색 점이 실데이터, 회귀선 위의 파란색 점이 회귀 모델의 예측값이다.
민트색 화살표는 데이터의 실제값과 평균의 차이(SST, 총 변동),
노란색 화살표는 예측값과 평균의 차이(SSR, 회귀선으로 설명되는 변동),
빨간색 화살표는 실제값과 예측값의 차이(SSE, 오차)를 의미한다.

변동성 지표를 면적으로 표현하면 다음과 같다.
빨간색 정사각형의 면적과 파란색 정사각형의 면적은 각각 SST와 SSE를 의미한다.

아래는 동일한 데이터셋에 대한 서로 다른 회귀 모델의 결정계수(R²) 값들을 비교한 그림이다.

첫 번째 그림처럼 회귀선이 모든 실데이터를 설명하는 경우는 거의 없다.
이런 경우 모델이 데이터에 과적합 되었을 가능성이 높다.
실제로 적합도가 높게 잘 나온 모델은 위 그림에서 Good, OK 정도의 결정계수를 가진다.
결정계수 값이 1에 가깝게 나온다면 과적합이 아닌지 의심해보아야 한다.
손실 함수(Loss Function)
(1) MSE(Mean Squared Error)
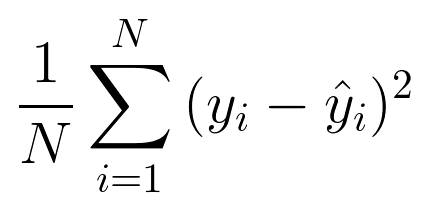
- 실제값과 예측값의 차이를 제곱한 값의 평균
- 회귀 모델에서 가장 많이 사용되는 성능 지표
- 작을수록 성능이 좋지만 과도하게 줄일 경우 과적합 발생 가능
- 성능을 평가하는 절대적인 기준이 없어, 다른 모델과 비교해야만 성능 평가 가능
(2) RMSE(Root Mean Squared Error)
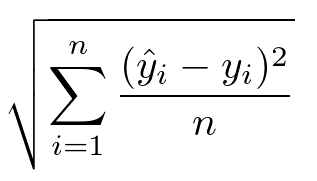
- MSE는 제곱의 평균이므로 데이터의 양이 많아지면 평균을 내더라도 값이 커지는 단점이 존재
- RMSE는 오차의 왜곡을 줄이기 위해 MSE에 루트를 씌워 값을 작게 한 것
- 값이 0에 가까울수록 좋은 모델
(3) MAE(Mean Absolute Error, 평균절대오차)
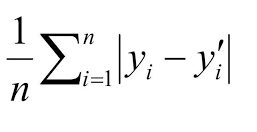
- 실제값과 예측값의 차이에 대한 절댓값의 평균
- 값이 낮을수록 우수한 모형
- 실제값과 예측값의 절대적 차이만 제공(상대적 차이에 대한 정보는 미제공)
(4) MAPE(Mean Absolute Percentage Error, 평균절대비율오차)
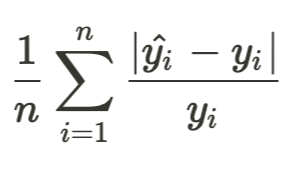
- 실제값에 대한 실제값과 예측값의 차이를 비율(%)로 측정
- 퍼센트 값을 가지며, 0에 가까울수록 좋은 모델
- 0과 100 사이의 값을 가지므로 이해가 용이
* MAE(평균절대오차)와 MAPE(평균절대비율오차)의 비교
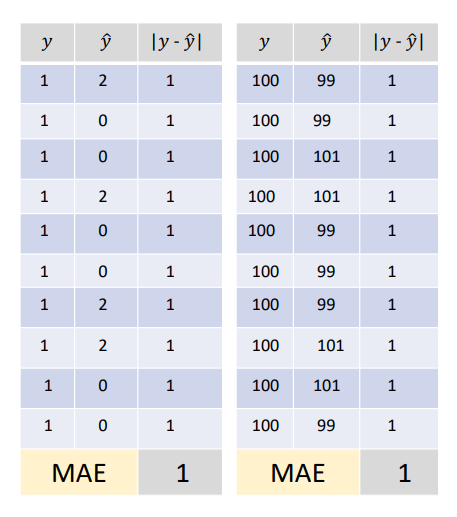
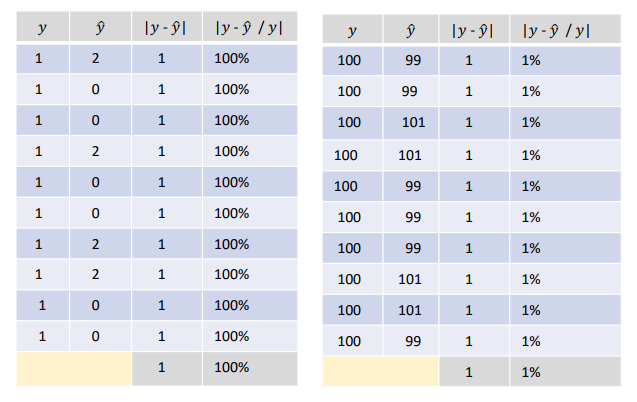
단순히 절대적인 차이만을 알고 싶으면 MAE, 상대적인 차이를 알고 싶으면 MAPE를 활용한다.
모델과 상황에 따라 적절한 평가 방식을 사용하는 것이 중요하다.
예를 들어 비슷한 취향을 가진 사람들의 영화 평점의 실제 평균이 1이고 예측값이 2인 경우와,
평균이 10이고 예측값이 9인 경우의 절대적인 오차 값인 MAE는 동일하다.
하지만 실제값에 대한 오차의 비율인 MAPE로 비교한다면,
MAPE가 각각 100%와 10%이므로 두 번째 모델의 성능이 훨씬 우수하다고 해석할 수 있다.
규제 선형 회귀(Regularized Linear Regression)
선형 회귀 모델에서 회귀 계수(W)의 값이 지나치게 커지는 과적합 현상을 방지하기 위하여,
규제(Regularization)를 적용하지 않은 일반 회귀 모델에 L2 또는 L1 규제를 추가하기도 한다.
이처럼 규제를 적용한 선형 회귀 모델을 규제 선형 회귀 모델이라고 한다.
- 릿지(Ridge) : L2 규제를 추가한 모형
- 라쏘(Lasso) : L1 규제를 추가한 모형
- 엘라스틱넷(ElasticNet) : L1, L2 규제를 결합한 모형
최적의 회귀 모델을 구현하기 위한 손실 함수의 구성 요소는 다음과 같다.
손실(비용) 함수의 구성 요소 = 학습 데이터 잔차 오류의 최소화 + 회귀 계수의 크기 제어
따라서 손실 값을 최소화하기 위해서는 오차 값을 줄이거나 회귀 계수의 크기를 낮춰야 한다.
오차가 최소화되는 회귀 계수를 찾는 것이 일반 선형 회귀 모델의 목적이라면,
하이퍼 파라미터(alpha)를 지정하여 회귀 계수의 크기까지 제어하는 것이 규제 모델의 목적이다.
L2 규제와 L1 규제는 회귀 계수/가중치(W) 제어 방식에 차이를 두고 있다.
(1) L2 규제(Ridge 모델)
비용 함수 목표 = min( 최소제곱합 + ( alpha x 가중치(W)의 제곱합 ) )
하이퍼 파라미터 alpha 값을 낮게 설정하면 모델은 최소제곱합(RSS)을 줄이고,
alpha 값을 높게 설정하면 모델은 회귀 계수(W)를 감소시키면서 두 항의 균형을 유지한다.
(2) L1 규제(Lasso 모델)
비용 함수 목표 = min( 최소제곱합 + ( alpha x 가중치(W)의 절댓값의 합 ) )
L1 규제의 경우 영향력이 크지 않은(회귀 계수가 0에 가까운) 회귀 계수의 값을 0으로 변환하여,
특정 feature 데이터가 모델에 반영조차 되지 않을 수 있다는 단점이 있다.
(3) ElasticNet 모델
ElasticNet 모델은 feature가 많은 데이터셋을 활용할 때 주로 사용하는 L1 & L2 규제 모델이다.
L1규제로 feature의 수를 줄이고, L2 규제로 회귀 계수의 크기를 조정한다.
주요 하이퍼 파라미터는 alpha와 l1_ratio이다.
- alpha : L1 규제의 alpha(a) + L2 규제의 alpha(b)
- l1_ratio : a / ( a + b )
* 0과 1 사이의 l1_ratio 값 적용
- l1_ratio = 0 : L2 규제와 동일
- l1_ratio = 1 : L1 규제와 동일
- 0 < l1_ratio < 1 : L1, L2 규제를 적절히 적용
실습에서는 모델의 alpha 값을 고정해놓고 l1_ratio 값을 수정해가면서 모델의 성능을 살펴본다.
규제 선형 회귀 모델과 하이퍼 파라미터 튜닝 관련 실습 코드는 아래 링크에서 확인할 수 있다.
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-12-regularization.ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 14. 분류(1): Logistic Regression (0) | 2022.06.29 |
|---|---|
| 13. Kaggle 프로젝트: 자전거 대여 수요 예측 (0) | 2022.06.29 |
| 11. 선형 회귀(1): 단순/다중 선형 회귀 (0) | 2022.06.20 |
| 10. 데이터 전처리: 인코딩, 스케일링 (0) | 2022.06.20 |
| 09. 교차 검증: cross_val_score, GridSearchCV (0) | 2022.06.20 |