회귀 모델은 연속적인 숫자 데이터의 예측 값을 찾는 모델이다.
이번 포스팅부터는 머신러닝 알고리즘을 다룬다.
머신러닝은 지도 학습, 비지도 학습, 강화 학습으로 나누어지는데,
이 중 지도 학습을 공부하고 있으며, 지도 학습에는 분류 모델과 회귀 모델이 있다.
이번에 알아볼 회귀 모델은 연속적인 데이터, 즉 숫자 데이터의 예측 값을 찾는 모델이다.
아래는 선형 회귀 모델의 예시이며, 좌표에 분포한 점들은 실제 데이터를 의미한다.
선형 회귀 모델의 목적은 가지고 있는 실데이터의 동향을 가장 잘 설명하는 직선을 찾는 것이다.


위의 예시에서 점의 분포에 맞는 직선을 찾아내면, 이를 토대로 8시간 이상 공부했을 때의 성적과
롤러코스터가 450m 이상의 높이에 도달했을 때의 최고 순간 속력을 예측할 수 있다.
회귀 모델에는 기본적으로 종속변수(target)와 설명변수(feature)가 존재한다.
- 종속변수(= 반응변수, target) : 예측의 대상이 되는 변수(설명변수에 의해 결정되는 변수)
- 설명변수(= 독립변수, feature) : 종속변수에 영향을 주는 변수
예를 들어 중고차 가격을 예측하는 모델에서 자동차의 가격이 종속변수가 되고,
연식, 주행거리, 유종, 마력 등 자동차의 가격을 결정하는 여러 가지 요소들이 설명변수가 된다.
가격이 미리 정해져 있는 여러 가지 데이터의 feature로 알고리즘을 학습시킨 후,
알고리즘에 새로운 테스트 데이터를 넣었을 때 자동차의 가격을 예측하는 것이 회귀 모델이다.
단순 선형 회귀(Simple Linear Regression)
단순 선형 회귀 모델은 독립변수와 종속변수가 각각 한 개씩 존재하는 모델이다.
종속변수의 예측값 y에 대한 독립변수 x가 하나만 존재하기 때문에,
y = Wx + b 형태의 최적의 직선 하나만 도출하면 된다.

직선의 기울기 W와 절편 b는 각각 알고리즘을 통해 학습하게 되는 파라미터이다.
단순 선형 회귀 모델의 목적은 학습을 통해 실제 값(정답 데이터)과 추정 값의 차이인
잔차의 합을 최소화하는 회귀 계수 W를 찾아 최적의 모델을 구현하는 것이다.
위 그림의 검은 점들이 실데이터, 회귀선과 점들 간의 거리인 빨간 선이 오차항(error term)이다.
* 모집단인 경우 오차(error), 표본집단/test 데이터인 경우 잔차(residual)라고 부른다.
좌표 위에 무수히 많은 직선이 그려질 수 있는데, 이 직선들 중에서 잔차의 합이 최소화되는,
즉 실데이터와 예측 값의 차이를 모두 더한 값이 가장 적은 직선이 최적의 직선이다.
잔차의 합은 아래와 같이 구할 수 있다.
y는 실제 데이터, ŷ는 추정 값을 의미한다.
추정 값이 더 큰 경우 음수가 상쇄되는 것을 방지하기 위해 제곱을 해준다.
Residual Sum of Squares(RSS) =

이처럼 데이터를 토대로 산출한 모델의 예측 값과 실제 값의 차이를 표현하는 지표를
손실 함수(Loss Function)라고 한다.
추가로 두 종류의 손실 함수를 간단히 알아보고 넘어가도록 하자.
모델 성능 평가에 활용되는 손실 함수는 다음 포스팅에서 자세히 살펴볼 예정이다.
(1) MSE(Mean Squared Error)
데이터의 양이 많아지면 절대적인 손실 값이 커지므로 전체 손실의 평균을 계산한다.

(2) RMSE(Root Mean Squared Error)
MSE는 오류의 제곱을 구하기 때문에 실제 오류의 평균보다 값이 커지는 특성이 있다.
오류 값의 왜곡을 줄이기 위해 MSE에 루트를 씌운 것이 RMSE이다.
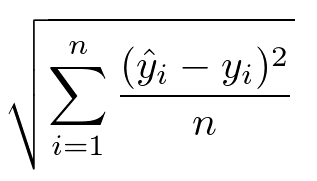
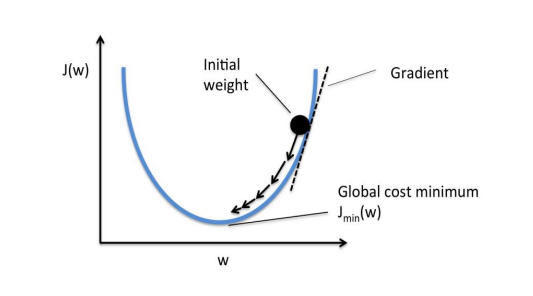
경사 하강법(Gradient Descent)
회귀 계수 W를 계속 바꿔가면서 오차를 최소화하는 최적의 회귀 계수를 찾아가는 방식이다.
(* 비용 함수를 최소화하기 위해 반복하여 파라미터를 조정해 나가는 것)
일반적으로는 1차 미분계수(기울기)를 이용하여,
이동 간격(Learning Step)을 조정하면서 함수의 최솟값을 찾아나가는 과정을 말한다.
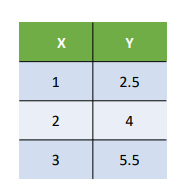
아래 예시에서 3개의 x에 대한 실제 데이터가 주어졌을 때,
W와 b의 초깃값을 임의로 각각 0.5와 1로 설정하고 W를 바꿔가면서 오차의 합을 구할 수 있다.
(y = Wx + b ← W, b 대입)
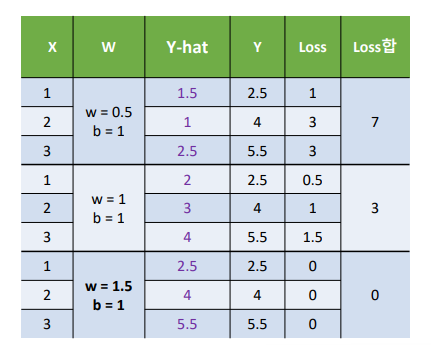
W = 1.5, b = 1일 때 오차의 합이 최소이다.
따라서 최적의 회귀 계수는 1.5이고, 이 경우 최적의 직선을 그릴 수 있다.
예시에서는 세 번에 불과하지만 컴퓨터는 무수히 많은 회귀 계수에 대한 계산을 빠르게 진행한다.
다중 선형 회귀(Multiple Linear Regression)
다중 선형 회귀 모델은 하나의 종속변수에 대한 독립변수가 여러 개 존재하는 모델이다.
실행활에서 독립변수가 하나인 경우는 거의 없다.
각각의 독립변수에 대하여 오차가 최소가 되는 W를 찾는 것이 다중 선형 회귀 모델이다.
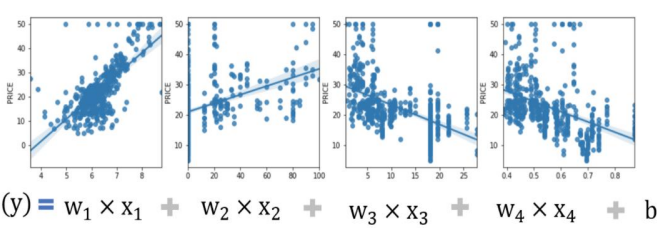
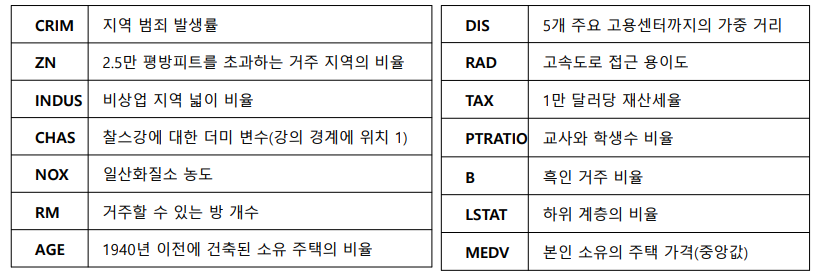
선형 회귀 모델 구현 실습에는 sklearn 라이브러리의 보스턴 주택가격 데이터셋을 사용한다.
13개의 feature로 주택가격(label)을 예측하는 회귀 분석용 데이터셋이다.
총 506 x 14 = 7084개의 데이터가 존재한다.
(1) 학습/테스트 데이터 분할
- train_test_split()
(2) 모델 객체 생성 및 학습
- LinearRegression() : sklearn.linear_model 모듈의 LinearRegression API
- fit(x_train, y_train) : 학습 데이터를 이용하여 모델의 회귀 계수(W)와 편향(b)을 학습
* 회귀 모델에서 fit()을 사용하는 것은 최적의 W를 찾아가는 것을 의미
(3) 예측 수행 및 성능 측정
- predict(x_test) : 모델에 학습에 쓰이지 않은 테스트 데이터를 입력하여 계산된 예측값 반환
- score(x_test, y_test) : 모델에 테스트 데이터를 입력하여 모델의 성능지표(R²) 반환
* 회귀 모델의 기본 성능 지표
연속적인 값을 다루는 회귀 모델은 데이터 하나하나의 예측 정확도를 구하기 어렵다.
회귀 모델의 성능은 결정계수(R²)와 손실 함수로 평가하며, 기본 성능 지표는 결정계수이다.
정확도(Accuracy)는 분류 모델의 성능 지표이다.
(4) 학습된 모델의 회귀 계수 확인
- coef_ : fit()을 통해 학습된 모델의 회귀 계수(W)가 저장된 변수
- intercept_ : bias(b)가 저장된 변수
아래 링크에서 회귀 분석 실습 코드를 확인할 수 있다.
1) 샘플 데이터
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-11-linear_regression_(1).ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
2) 보스턴 주택가격 예측
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-11-linear_regression_(2).ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
3) 중고차 가격 예측(KNN/Linear regression)
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-11-linear_regression_(3).ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 13. Kaggle 프로젝트: 자전거 대여 수요 예측 (0) | 2022.06.29 |
|---|---|
| 12. 선형 회귀(2): 성능 평가 지표와 규제 선형 회귀 (0) | 2022.06.29 |
| 10. 데이터 전처리: 인코딩, 스케일링 (0) | 2022.06.20 |
| 09. 교차 검증: cross_val_score, GridSearchCV (0) | 2022.06.20 |
| 08. 머신러닝 라이브러리: Scikit-learn (0) | 2022.06.20 |