Logistic Regression 모델은 선형 회귀 개념을 기반으로 한 분류 모델이다.
가장 기본적인 분류 모델인 로지스틱 회귀(Logistic Regression)는 선형 회귀 기반의 모델이다.
선형 회귀 모델은 연속적인 수치 값을 예측하는 것을 목적으로 하는데,
분류 목적의 데이터는 값이 연속적이지 않고 0과 1의 이진 데이터 형태를 띤다.
가령 나이를 독립변수로, 암이 맞는지(1) 아닌지(0) 여부를 종속변수로 가지는 데이터에
선형 회귀 모델을 적용하면 아래와 같은 회귀선을 도출할 수 있다.

이진 형태의 데이터로도 선형 회귀 알고리즘 생성 및 회귀선 도출이 가능하지만,
직선이 좌표 위의 점들을 잘 설명한다고 보기는 어렵다.
이처럼 선형 회귀 개념의 적용이 어려운 이진형 종속변수에 대하여,
회귀식의 형태로 분류와 추정이 가능하도록 하는 것이 로지스틱 회귀 모델의 목적이다.
로지스틱 회귀(Logistic Regression) 도출 과정
어떻게 선형 회귀의 개념으로부터 로지스틱 회귀 분류 모델을 이끌어냈는지 알아보려고 한다.
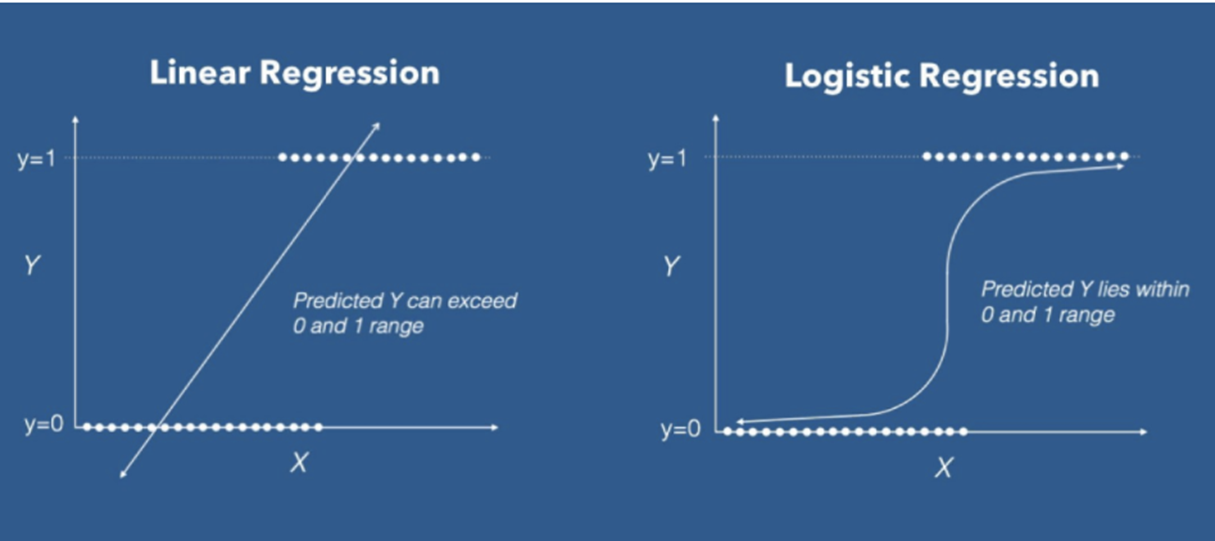
선형 회귀 모델의 경우 종속변수의 범위가 [-∞, ∞]이다.
종속변수가 0과 1의 값만을 가지는 이진형 데이터일 경우 선형 회귀 모델을 적용할 수 없다.
따라서 종속변수의 범위를 [-∞, ∞]로 변환해주기 위한 과정을 거친다.
(1) 확률값으로의 변환
이진값을 [0, 1]의 범위를 가지는 확률값으로 변환한다.
종속변수가 0 또는 1이 될 확률은 모두 [0, 1] 범위의 값을 가진다.
(2) 승산(Odds) 개념 적용
승산(Odds)은 실패 확률에 대한 성공 확률을 말한다.
p가 성공 확률을 의미할 때, 승산을 수식으로 나타내면 다음과 같다.

확률값 p가 0에서 1로 변화함에 따라 승산은 0부터 무한대의 값을 가진다.
이진값을 [0, 1] 범위의 확률값으로, 이를 다시 승산으로 변환하면 종속변수의 범위는 [0,∞]이다.

(3) 로그 변환
승산에 로그를 취하면 범위의 제약이 없어진다.
즉, 이 경우 종속변수의 범위는 [-∞,∞]이다.
선형 회귀식의 값과 범위가 동일해졌으므로 선형 회귀 개념을 적용할 수 있다.

log(Odds) 값을 선형 회귀식의 형태로 놓고 지수 변환하여 확률값 p에 대해 정리할 수 있다.

↓

↓

확률값 p가 [0, 1] 범위를 가지므로 p에 대해 정리한 식을 공역이 [0, 1]인 함수로 이해할 수 있다.
이러한 형태의 함수를 시그모이드(Sigmoid) 함수라고 한다.
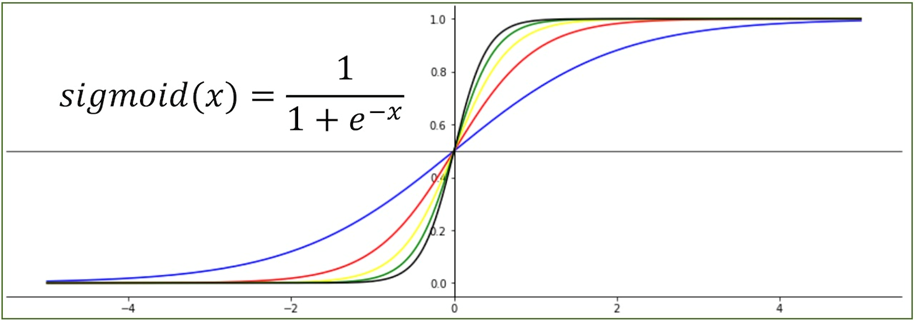
* 로지스틱 회귀(Logistic Regression)
- 독립변수의 선형 결합을 이용하여 사건의 발생 가능성(확률)을 예측하는 데 사용되는 기법
- 선형 회귀 방식을 분류 분석에 적용한 알고리즘
- 두 개의 카테고리를 가지는 이진 형태의 종속변수를 예측
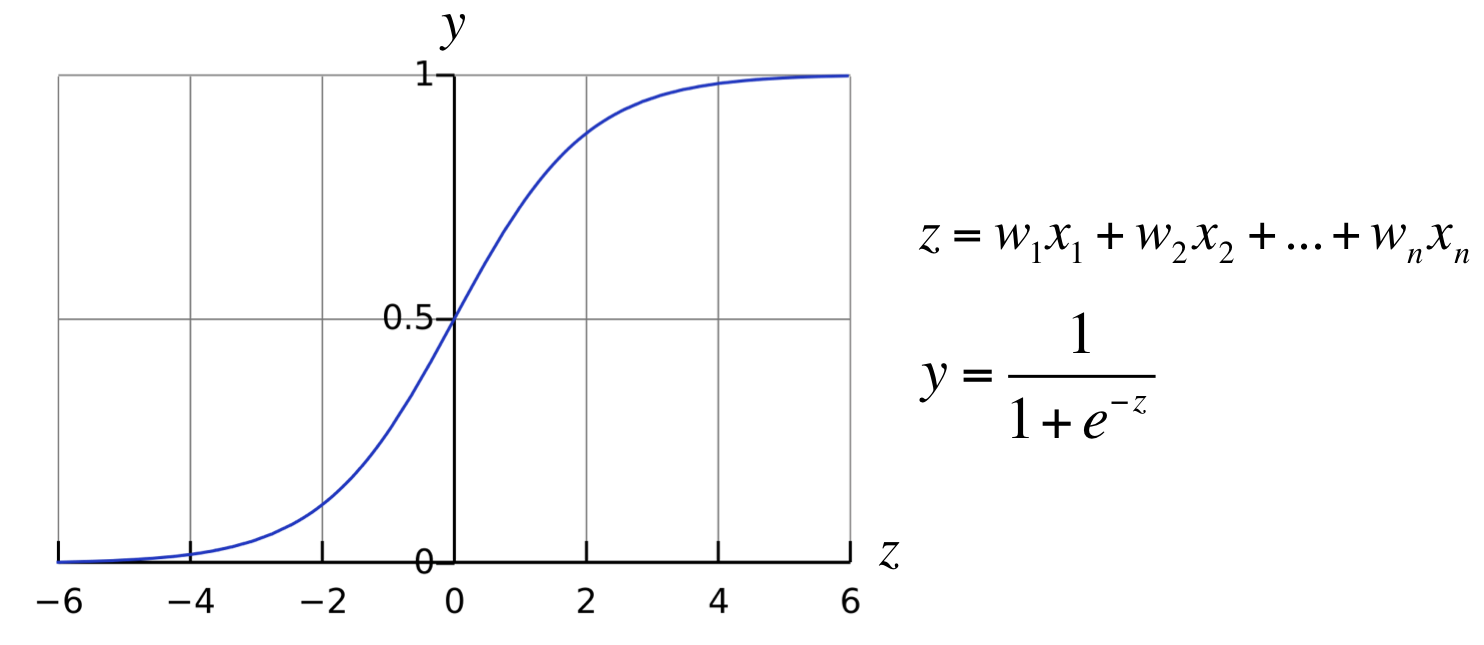
로지스틱 회귀 모델은 학습을 통해 선형 함수의 회귀 최적선을 찾는 것이 아니라,
시그모이드 함수의 최적선을 찾고 이 함수의 반환값 y = sigmoid(x)를 확률로 간주한다.
0 또는 1의 값을 가지는 종속변수가 0이 될 확률과 1이 될 확률을 비교해 분류를 결정한다.
종속변수의 확률 범위 [0, 1]에서 시그모이드 함수가 반환한 확률값이 임계값 이상이면 positive,
임계값 미만이면 negative 클래스를 예측한다. (일반적으로 임계값 0.5 사용)
로지스틱 회귀 모델은 선형 회귀 모델처럼 y에 대한 예측값을 그대로 종속변수로 쓰지 않고,
예측값에 대한 로지스틱(시그모이드) 함수를 회귀식의 종속변수로 사용한다.
즉, 독립변수 x에 선형 회귀를 적용한 값을 다시 시그모이드 함수에 전달하여 도출된 값이다.
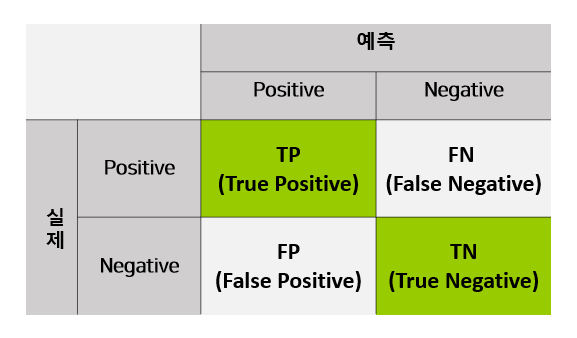
오차 행렬(Confusion Matrix)
오차 행렬 또는 정오 행렬은 분류 모델의 예측 결과를 나타내는 행렬로,
이진 분류에서 모델이 예측을 수행하며 얼마나 혼동하고 있는지를 보여주는 지표로 사용된다.
분류 모델의 예측 결과는 네 가지로 구분할 수 있다.
(1) 예측이 맞은 경우
- TP(True Positive) : 예측값, 실제값 positive 일치
- TN(True Negative) : 예측값, 실제값 negative 일치
(2) 예측이 틀린 경우
- FP(False Positive) : 예측값 positive, 실제값 negative
- FN(False Negative) : 예측값 negative, 실제값 positive
예측 결과를 나타내는 두 개의 알파벳 중 앞의 글자는 예측이 맞았는지 여부를,
뒤의 글자는 예측값이 positive(1), negative(0) 중 어느 것인지를 보여준다.
여기서 positive, negative는 상대적인 개념이다.
예를 들어 암이 맞는지 아닌지를 판단하는 데이터를 가지고 있을 때,
암 진단을 받은 사람의 데이터가 더 중요하다면 암이 맞는 경우의 target을 1로 설정할 수도,
암이 아닌 사람의 데이터가 더 중요하다면 암이 아닌 경우의 target을 1로 설정할 수도 있다.
어떤 경우이든 알고리즘은 주어진 학습 데이터의 기준에 맞게 분류를 진행한다.
분류 모델의 예측 결과를 2 x 2 행렬로 나타낸 것이 오차 행렬(Confusion Matrix)이다.
분류 모델의 성능 지표
(1) 정분류율(Accuracy)
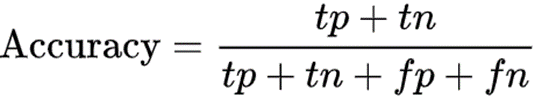
(2) 정밀도(Precision)
- 모델에서 정답이 아닌 것을 얼마나 잘 걸러내는지 보여주는 지표
- 예측값이 positive인 데이터(predicted positive) 중 예측이 맞은 것의 비율
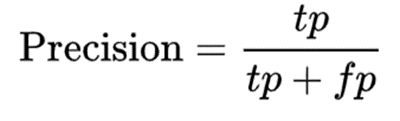
(3) 재현율(Recall), 민감도(Sensitivity/TPR)
- 모델에서 실제 정답을 얼마나 많이 선택하는지 보여주는 지표
- 실제값이 positive인 데이터(actual positive) 중 예측이 맞은 것의 비율
- 모델의 완전성을 평가하는 지표(actual positive를 정확하게 예측하는 능력)
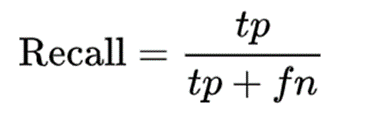
이외에도 특이도(Specificity/TNR)가 있는데, 이후에 자세히 다룰 예정이므로 참고만 해둔다.
- tn / ( tn + fp )
- 실제값이 negative인 데이터(actual negative) 중 예측이 맞은 것의 비율
대부분의 경우 정분류율(Accuracy)로 분류 모델의 성능을 평가한다.
하지만 정밀도(Precision)와 재현율(Recall)이 어떤 경우에 쓰이는지 알아두고,
상황에 따라 필요한 성능 지표를 선택하여 사용할 줄 아는 것이 중요하다.
예를 들어 1000명 중 10명(10%)의 암 환자를 진단하는 모델을 구축했을 때,
암 진단 모델이 정상인 사람과 암 환자를 아래와 같이 분류했다고 하자.
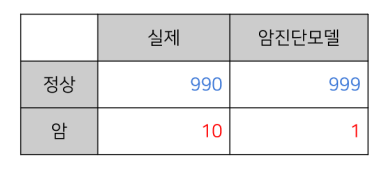
암 환자인 경우를 positive, 암 환자가 아닌 경우를 negative로 놓았다면,
암 진단 모델의 오차 행렬(Confusion Matrix)은 다음과 같다.
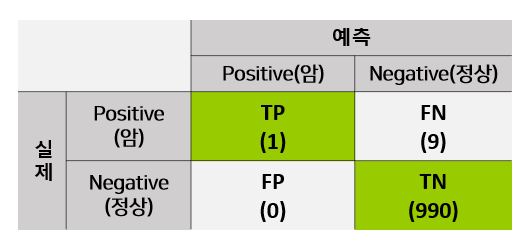
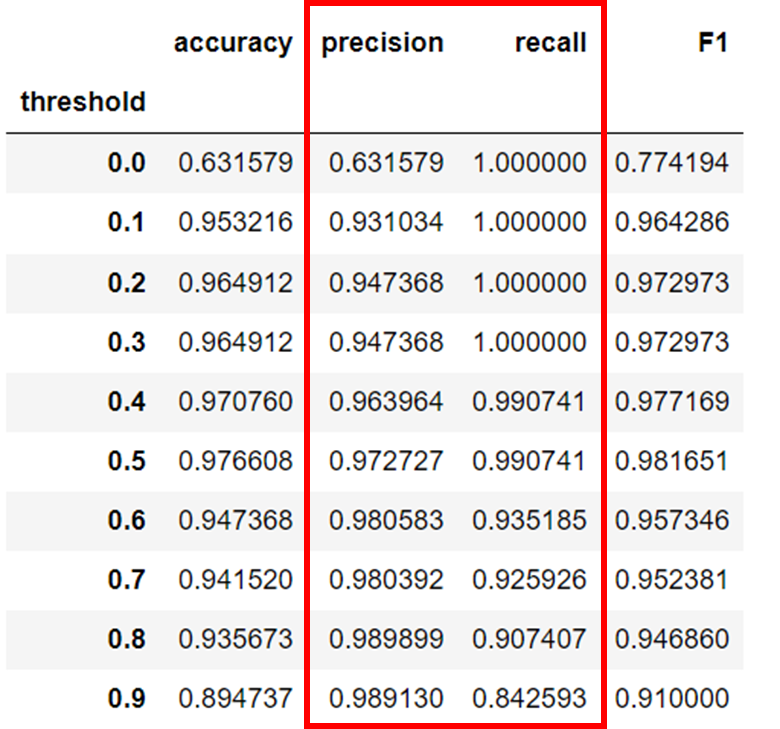
- Accuracy : (1 + 990) / 1000 = 99.1%
- Precision : 1 / (1 + 0) = 100%
- Recall : 1 / (1 + 9) = 10%
정분류율(Accuracy)과 정밀도(Precision)이 매우 높게 측정된 것을 볼 수 있다.
하지만, 이 모델의 주 목적은 암 진단이라는 것에 주목할 필요가 있다.
실제 암 진단에 사용되었다면 암 환자만 놓고 봤을 때 10명 중 9명은 치료 시기를 놓쳤을 것이다.
따라서 이 모델은 성능 지표가 낮은 모델로 보는 것이 설득력 있는 해석이다.
정밀도와 재현율의 차이가 크다면 대부분의 경우 재현율로 모델을 평가한다.
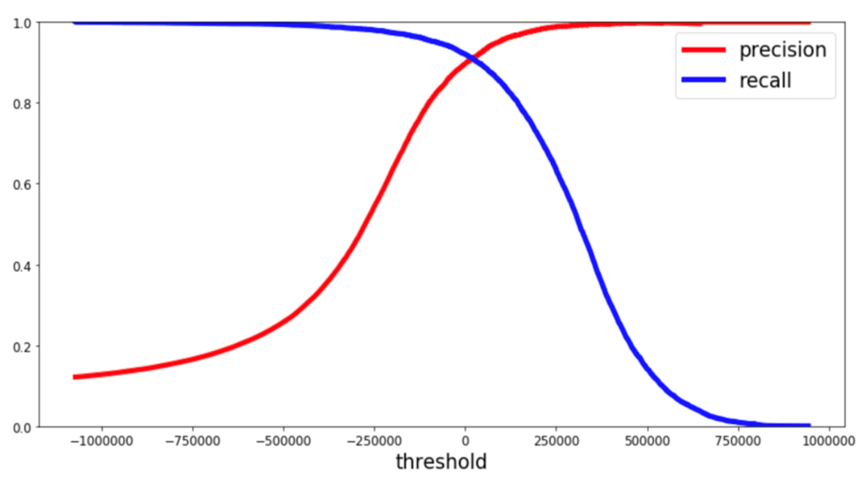
* 정밀도(Precision)와 재현율(Recall)의 트레이드 오프
정밀도와 재현율은 반비례 관계의 상호 보완적인 성능 평가 지표이다.
(4) F1 Score
- 정밀도와 재현율의 조화 평균을 나타내는 지표
- Precision, Recall 중 어느 한 쪽으로 치우치지 않은 때에 높은 값을 산출
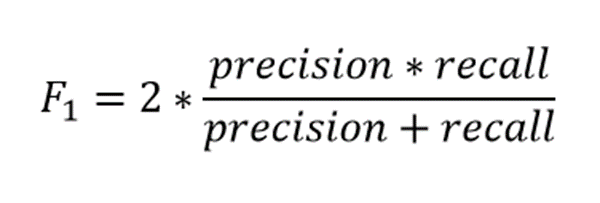
정밀도와 재현율 중 어떤 성능 지표를 살펴봐야 할지 확실하지 않을 때 F1 Score를 참고한다.
두 지표를 따로 살펴보지 않고 F1 Score로 한 번에 보는 경우가 많다.
* 분류 평가 지표 선택 가이드라인
균형 잡힌 데이터라면 정분류율이나 균형정확도(BCR, Balanced Correction Rate)를 사용한다.
반면, 클래스 데이터에 범주의 불균형이 존재한다면 F1 Score를 주로 사용한다.
특히 불균형한 클래스 데이터 값 중 보다 중요한 범주가 존재하는 경우 F1 Score가 유용하다.
예를 들어 신용카드 사기 데이터나 암 진단 데이터를 생각해보자.
신용카드 사기 피해자와 암 환자의 비율이 그렇지 않은 경우에 비해 훨씬 적지만,
사기 피해와 암을 예방하는 것이 매우 중요하기 때문에 F1 Score를 높게 유지할 필요가 있다.
마지막으로 3개 이상의 범주를 가진 데이터를 분류하는 경우, 다음과 같이 성능 지표를 산출한다.
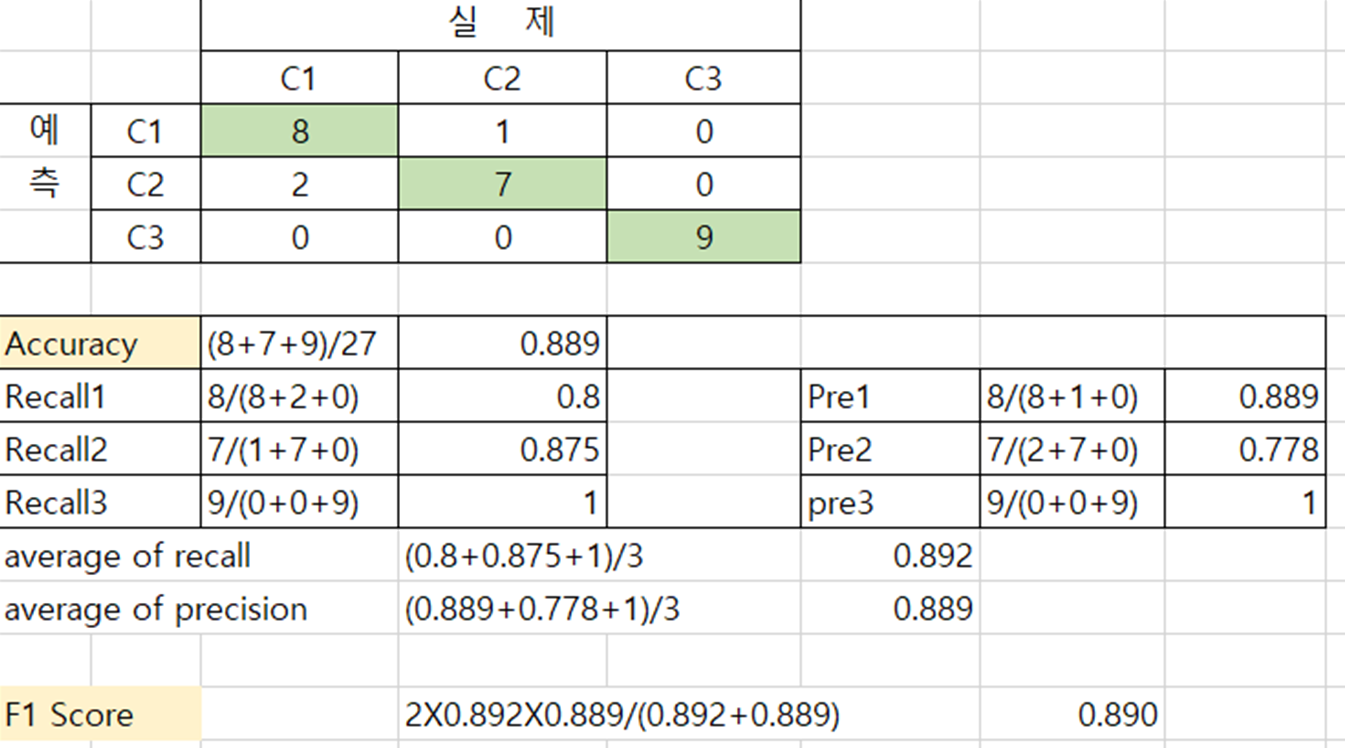
실제와 예측이 일치한 연두색 셀은 정분류율(Accuracy)를 산출할 때 사용되며,
Recall/Pre 1, 2, 3은 각각 C1, C2, C3의 재현율(Recall)과 정밀도(Precision)이다.
이들을 평균 낸 것이 최종 Recall, Precision이며, F1 Score 산출에 사용된다.
ROC(Receiver Operating Characteristic) Curve
ROC 곡선은 가능한 모든 cut-off(임계값, threshold)에 대한 TPR/FPR을 산출하여,
가로축을 FPR, 세로축을 TPR로 두고 시각화한 2차원 그래프이다.
* TPR = True Positive Rate(민감도), FPR = False Positive Rate(1 - 특이도)
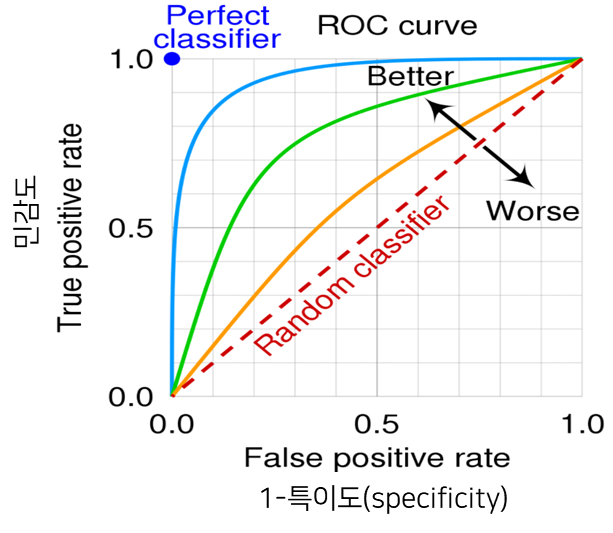
곡선이 Random Classifier(기울기 1, TPR = FPR) 위쪽에 위치하면 성능이 괜찮은 모델이다.
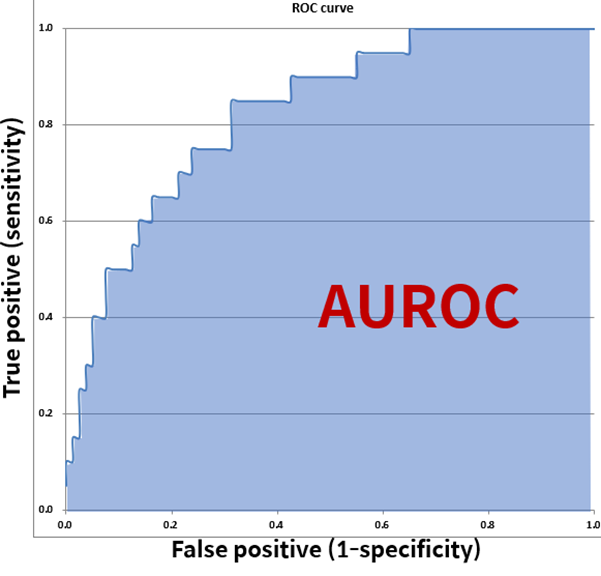
ROC 곡선은 이진 분류에서 주로 사용되는 성능 지표이다.
AUC(Area Under Curve) 또는 AUROC(Area Under ROC)는 ROC 곡선 아래의 면적을 말한다.
ROC 곡선 아래의 면적이 클수록(1에 가까울수록) 성능이 좋은 모델이다.
여기까지가 로지스틱 회귀(Logistic Regression) 모델과 분류 평가 지표에 대한 내용이다.
분류 모델 실습에는 유방암 진단 데이터셋(이진 분류, feature 30개)을 이용한다.
분류 계열의 알고리즘은 보통 표준화 작업이 필요하지 않다.
데이터의 분포가 모델의 성능에 크게 영향을 미치거나 결과를 좌지우지하지 않기 때문이다.
다만, 로지스틱 회귀 모델은 선형 회귀 기반의 알고리즘이므로 데이터 전처리가 필요할 수 있다.
실습에도 데이터의 분포를 정규분포형으로 변환해주는 등 전처리 과정이 포함되어 있다.
아래 링크에서 로지스틱 회귀(Logistic Regression) 모델 실습 코드를 확인할 수 있다.
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-14-logistic_regression.ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 16. 분류(3): Ensemble (0) | 2022.07.05 |
|---|---|
| 15. 분류(2): Decision Tree (0) | 2022.07.05 |
| 13. Kaggle 프로젝트: 자전거 대여 수요 예측 (0) | 2022.06.29 |
| 12. 선형 회귀(2): 성능 평가 지표와 규제 선형 회귀 (0) | 2022.06.29 |
| 11. 선형 회귀(1): 단순/다중 선형 회귀 (0) | 2022.06.20 |