군집 분석은 알고리즘이 스스로 라벨링 되지 않은 데이터를
분류하고 유사한 데이터끼리 묶는 비지도 학습 방식이다.
머신러닝에는 두 가지 모델 학습 방식이 존재한다.
사전에 제공된 정답(레이블) 데이터를 바탕으로 학습하는 지도 학습(Supervised Learning)과,
정답이 없는 데이터의 패턴을 스스로 찾아 학습하는 비지도 학습(Unsupervised Learning)이다.
지도 학습에는 분류(Classification)와 회귀(Regression) 모델이 있다.
이번 포스팅에서 다루게 될 군집화(Clustering)는 비지도 학습에 해당한다.
군집화(Clustering)
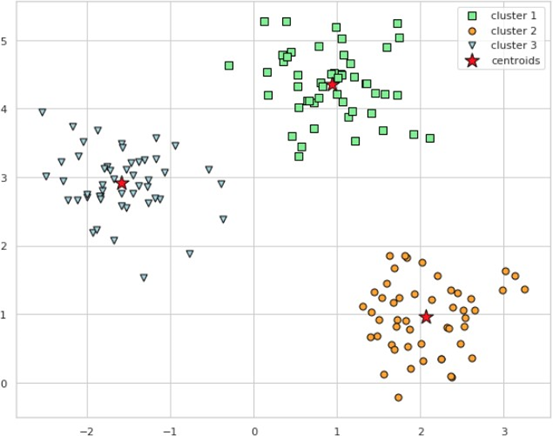
군집 분석에서 동일한 군집에 소속된 관측치들은 서로 유사할수록,
다른 집단에 소속된 관측지들은 유사하지 않을수록 군집화 모델의 성능이 좋다.
군집/관측치의 유사도는 관측치들 간의 거리나 상관계수로 정의한다.
군집 중심점(Centroid) 또는 밀도(Density)를 활용한 군집화 방식이 존재한다.
* 군집화 알고리즘
- K-Means(Centroid-based)
- DBSCAN(Density-based)
다음과 같은 경우에 군집화를 적용할 수 있다.
- 유사한 추세를 나타내는 주식 종목 그룹화
- 고객 행동 패턴, 브랜드, 마켓 세분화(Segmentation)
- 이미지 검출
- 이상 검출(Anomaly Detection)
실루엣 계수(Silhouette Coefficient)
실루엣 계수는 특정 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 위치해 있고,
다른 군집의 데이터와 얼마나 멀리 떨어져 있는지를 나타내는 지표이다.
0부터 1까지의 값을 가지며, 1에 가까울수록 Clustering의 품질이 좋다.
실루엣 계수가 0이면 의미 없는 군집화이고, 음수이면 잘못 분류된 것을 의미한다.

- a(i) : 개체 i와 같은 군집 내에 있는 모든 다른 개체들 사이의 평균 거리
- b(i) : 개체 i와 다른 군집에 있는 개체들 사이의 평균 거리 중 가장 작은 값

* 개별 객체의 실루엣 계수(Silhouette Coefficient) 산출

a(i) = 1.04
b(i) = min(10.4, 6.4) = 6.4

전체 데이터에 대한 실루엣 지표는 모든 군집에 속한 개별 객체의 실루엣 지표의 평균과 같다.

실루엣 분석(Silhouette Analysis)에는 sklearn.metrics 모듈이 사용된다.
* Method
- silhouette_samples(X, labels) : 각 데이터 포인트의 실루엣 계수를 산출
- silhouette_score(X, labels) : 전체 데이터의 실루엣 지표를 반환(개별 지표의 평균)
K-Means Clustering
임의의 군집 중심점(Centroid) 설정 후 가까운 점들을 모으는 Centroid-based 알고리즘으로,
자주 쓰이고 어렵지 않은 군집 분석 기법이다.
사전에 군집의 수 K가 정해져야 알고리즘 실행이 가능하다.
각 개체는 가장 가까운 중심에 할당되며, 같은 중심에 할당된 개체들이 하나의 군집을 생성한다.
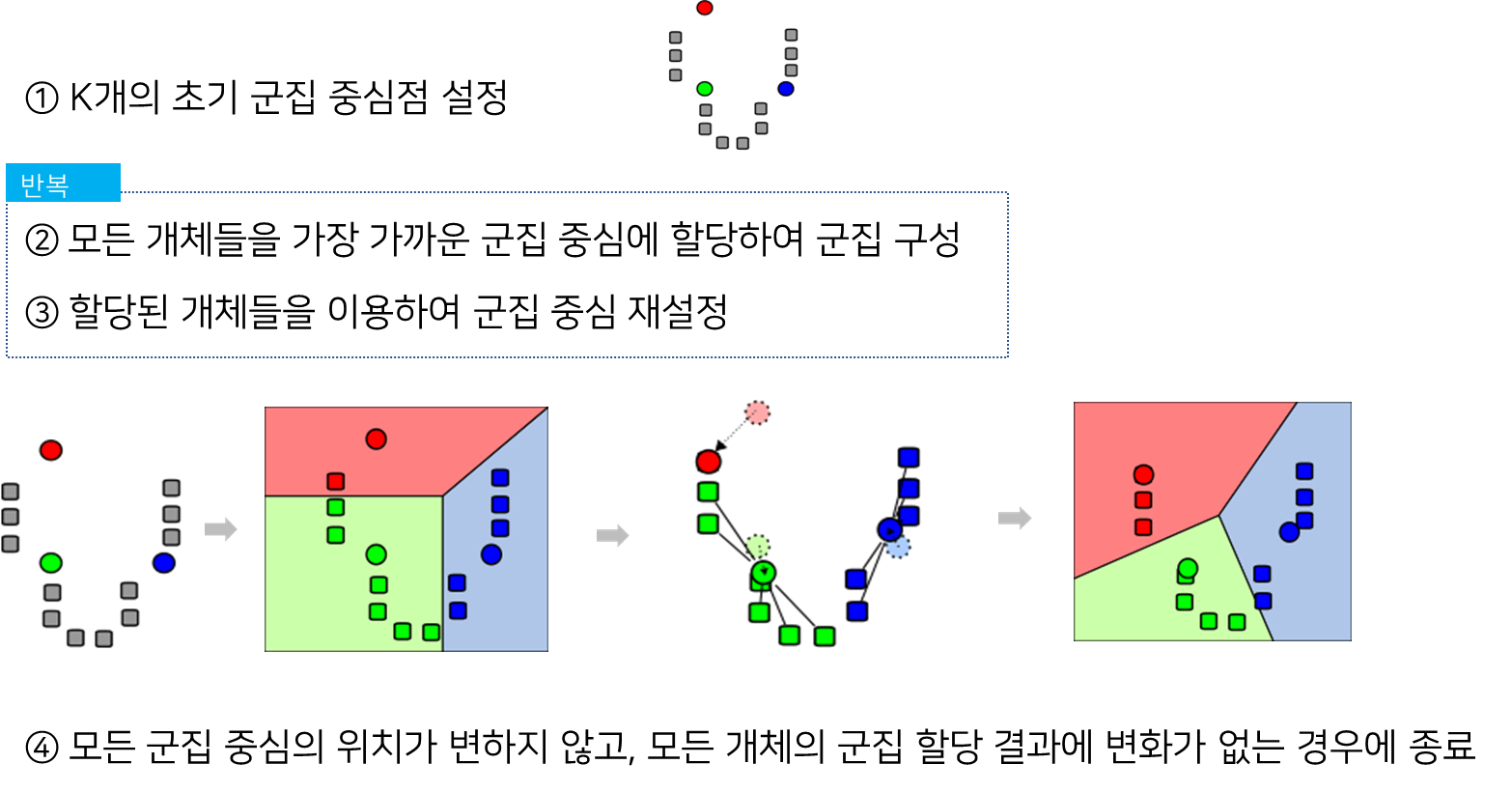
* K-Means 알고리즘 동작 과정
초기 군집 중심점 설정은 랜덤으로 또는 알고리즘의 계산에 의해 이루어진다.
K-Means 알고리즘은 쉽고 간결하며 대용량 데이터에도 활용이 가능하다는 장점이 있어,
일반적으로 군집화 작업에서 가장 많이 사용된다.
다만 초기에 몇 개의 군집 중심점을 설정해야 하는지에 대한 명확한 기준이 없고,
거리 기반의 알고리즘이므로 이상치(Outlier)에 취약하다는 단점이 있다.
K-Means Clustering에는 sklearn.cluster 모듈의 KMeans API를 사용한다.
* Argument
- n_cluster : 군집 중심점의 개수
- init : 초기에 군집 중심점의 좌표를 설정하는 방식(일반적으로 K-Means++ 방식 사용)
- max-iter : 최대 반복 횟수(도달 전에 모든 데이터의 중심 이동이 다 이루어지면 그대로 종료)
군집 중심점의 좌표는 랜덤으로 설정할 수도, 내부 알고리즘을 통해 설정할 수도 있다.
K-Means++ 알고리즘은 기존의 K-Means 알고리즘을 개선한 알고리즘이다.
K-Means 알고리즘은 모든 중심을 랜덤하게 위치시키므로 매번 결과가 달라질 수 있다.
또, 한 번에 K개의 중심을 랜덤하게 생성하여 중심 간 거리가 가까우면 성능이 저하될 수 있다.
K-Means++의 경우 K개의 중심을 한 번에 생성하지 않고 데이터 중 하나를 무작위로 선택하여,
해당 데이터 포인트를 첫 번째 중심으로 지정한 후 최대한 거리가 먼 곳에 다음 중심을 생성한다.
이 같은 방식으로 한 번에 하나씩 K번에 걸쳐 K개의 군집 중심점을 설정한다.
* Method
- fit_transform(dataset) : 학습 데이터를 이용하여 모델 학습
* Attribute
- labels_ : 각 데이터 포인트가 속한 군집 중심점 레이블
- cluster_centers_ : 각 군집 중심점의 좌표(shape=[군집 개수, feature 개수])
- inertia_ : 군집 내의 거리의 합(최적의 K를 찾을 때 사용)
군집 중심점의 좌표 위치를 시각화할 때 cluster_centers_를 사용할 수 있다.
최적의 K 결정
앞서 말한 것처럼 K-Means Clustering은 군집 중심점의 개수를 모른다는 단점이 있다.
최적의 K(군집 중심점의 개수)를 찾는 것이 K-Means의 가장 중요한 단계이다.
이를 도와주는 방법으로 Elbow method와 Silhouette method가 있다.
(1) Elbow method
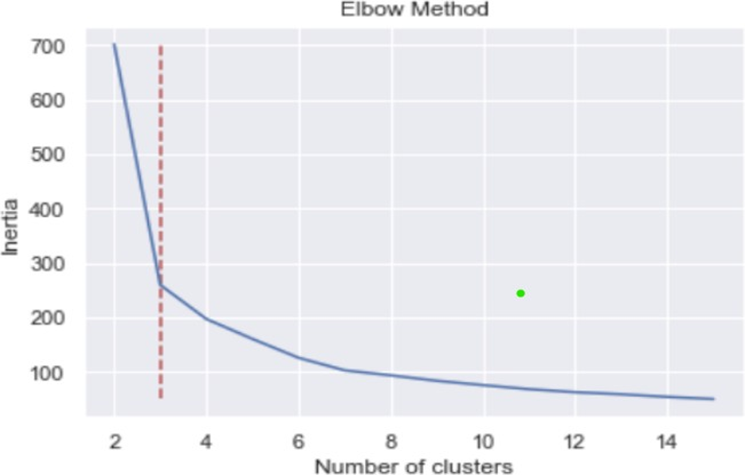
Total intra-cluster variation/Total within-cluster sum of squared distance(WCSS)가
최소가 되는 K를 찾는 방법으로, 군집 내의 거리의 합(변동성)을 나타내는 inertia가 급감하는
지점(Elbow)을 군집의 개수로 사용한다.
변동성이 급격히 떨어진다는 것은 유사한 데이터가 잘 묶였다는 것을 의미한다.
inertia 수치는 K-Means API의 inertia_ 속성으로 확인할 수 있다.
(2) Silhouette method
Elbow method를 사용하다 보면 inertia 그래프가 꺾이는 지점이 여러 개인 경우가 존재하므로,
최적의 K를 결정할 때 어느 정도 감에 의존할 수 밖에 없다.
따라서 실루엣 계수의 시각화를 통해 K를 최적화하는 Silhouette method를 함께 사용한다.
실루엣 계수는 군집 내의 거리와 군집 간의 거리를 모두 고려하기 때문에 참고하기 좋은 지표이다.
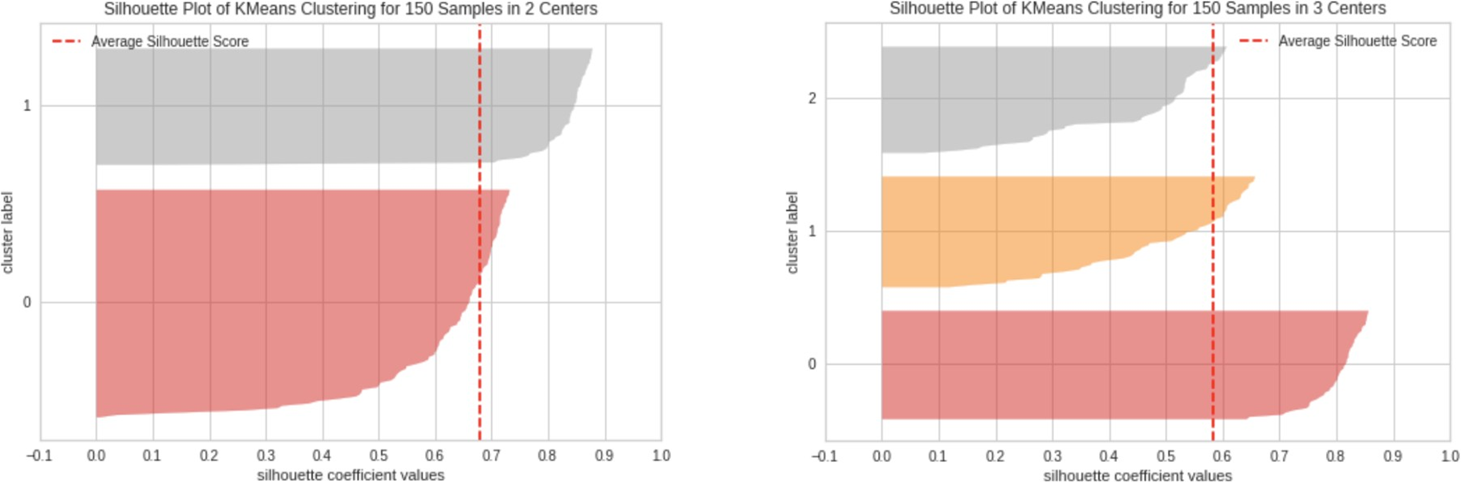
위의 그림에서 x축은 실루엣 계수, y축은 개별 군집과 이에 속하는 데이터이다.
빨간색 점선은 전체 데이터의 평균 실루엣 계수를 나타낸다.
개별 군집(y축)의 높이를 통해 군집 내 데이터의 분포와 뭉쳐 있는 정도를 가늠할 수 있다.
군집 중심점의 개수를 두 개로 설정한 왼쪽의 경우 평균 실루엣 계수가 0.7보다 조금 작다.
1번 군집의 데이터는 평균보다 높은 실루엣 계수를 가지지만,
0번 군집의 경우 대부분의 데이터가 평균 이하의 실루엣 계수를 가지며, 그림이 넓게 분포한다.
1번 군집은 내부 데이터가 뭉쳐있지만 0번 군집은 내부 데이터 간 거리가 멀다고 해석할 수 있다.
오른쪽 그림은 군집 중심점의 개수를 세 개로 설정한 경우이다.
평균 실루엣 계수 값은 두 개의 군집 중심점을 생성했을 때보다 작다.
0번 군집의 경우 모두 평균보다 높은 실루엣 계수를 가지는 것으로 보아 데이터가 잘 뭉쳐있지만,
1번과 2번 군집의 데이터는 대체로 평균보다 낮은 실루엣 계수를 가진다.
이상치에 취약한 군집화 모델의 특성 상 전체 데이터의 평균 실루엣 계수는 쉽게 변동할 수 있다.
따라서 평균 실루엣 계수와 개별 군집의 높이를 복합적으로 따져서 최적의 K를 결정한다.
개별 군집 간 적당한 거리를 유지하면서 군집 내 데이터가 잘 뭉쳐있는 경우를 찾는다.
여기까지 군집 분석에 대한 설명을 마친다.
실루엣 분석(Silhouette Analysis)과 K-Means 군집화 실습 코드는 아래 링크에서 볼 수 있다.
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-20-k-means_clustering.ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 19. 차원 축소 및 주성분 분석(PCA) (0) | 2022.07.05 |
|---|---|
| 18. Kaggle 프로젝트: 호텔 예약 (0) | 2022.07.05 |
| 17. 회귀 모델 성능 비교 (0) | 2022.07.05 |
| 16. 분류(3): Ensemble (0) | 2022.07.05 |
| 15. 분류(2): Decision Tree (0) | 2022.07.05 |