Decision Tree 모델은 데이터의 패턴을 학습하여
트리 기반의 분류 규칙을 생성하는 모델이다.
독립변수와 종속변수의 선형관계성에 기반한 로지스틱 회귀(Logistic Regression) 외에도
대표적인 분류 알고리즘이 몇 가지 더 존재한다.
- Naive Bayes(나이브 베이즈) : 베이즈 통계에 기반
- Decision Tree(의사결정나무) : 데이터 균일도에 따른 규칙에 기반
- SVM(Support Vector Machine) : 개별 클래스 간 최대 분류 마진을 찾는 알고리즘
- Ensemble(앙상블) : 서로 다른 머신러닝 알고리즘을 결합
- Artificial Neural Network(인공신경망)
앞으로의 포스팅에서 이들 중 Decision Tree 모델과 Ensemble 모델을 살펴볼 예정이다.
Decision Tree
Decision Tree 모델은 학습을 통해 데이터의 규칙을 찾아내 트리 기반의 분류 기준을 생성한다.

가장 위의 시작점을 Root node, 이후의 분기점들을 Decision node라고 한다.
Decision Tree 가장 아래에 위치하는 노드는 Leaf node이다.
Decision Tree 모델에서 데이터는 특정 기준에 따라 아래로 분류되어 내려간다.
트리가 가지를 뻗치는 깊이를 depth라고 하는데, Root node는 depth 0의 노드이다.
위 모형에서 Leaf 1, 4, 5는 depth 2의 노드이고 Leaf 2, 3는 depth 3의 노드이다.
CART(Classification and Regression Tree)
CART(Classification and Regression Tree)는 개별 변수의 영역을 반복적으로 분할함으로써
전체 영역에서의 규칙을 생성하는 재귀적 분기 기법으로, Decision Tree 알고리즘의 일종이다.
If, else 형식으로 표현되는 규칙을 생성하며,
범주형 변수와 수치형(연속형) 변수에 대한 처리가 동시에 가능하다.
- 범주형 변수 - 분류 트리
- 연속형 변수 - 회귀 트리
CART 기법에서는 분할 후 각 영역에 특정 객체가 다수 존재하도록 분할하는 것이 좋다.
아래 색깔 분류 예시에서 왼쪽 그림이 더 분류가 잘 된 것을 눈으로 확인할 수 있다.

알고리즘은 종속변수가 범주형 변수인 Decision Tree의 분류 규칙을 생성하기 위해
지니 계수, 엔트로피 지수 등의 불순도 지표와 카이제곱 통계량 등을 활용한다.
포스팅에서는 지니계수를 활용한 분류 방식을 알아본다.
지니 계수(Gini Coefficient/Gini Impurity)
지니 계수는 노드의 불순도를 나타내는 불순도 지표로, 값이 작으면 분류가 잘 되었다고 판단한다.

c개의 범주가 존재하는 특정 영역에 대한 지니 계수를 구하는 공식은 다음과 같다.
p는 k 범주에 속하는 레코드의 비율을 의미한다.

아래 그림과 같이 6개의 파란색 공과 10개의 빨간색 공이 섞여 있는 상태의 불순도는 0.469이다.

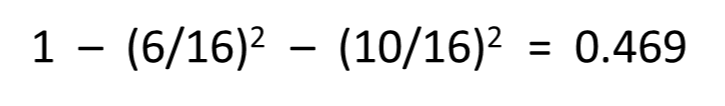
데이터의 범주가 두 개 뿐이라면, 모든 객체들이 동일한 범주에 속하는 경우의 지니 계수는 0,
객체들이 각각 1/2의 비중으로 존재하는 경우의 지니 계수는 0.5이다.
지니 계수를 활용한 데이터 분류 예시
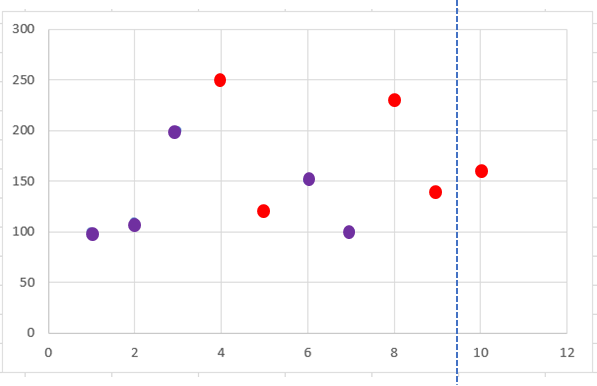
공부시간과 학원비를 feature로 합격 여부를 판단하는 데이터가 있다.
좌표 위의 빨간색 점은 합격 데이터, 보라색 점은 불합격 데이터이다.
먼저 공부시간을 기준으로 데이터를 오름차순 정렬한 후 공부시간을 분기의 기준변수로 사용한다.
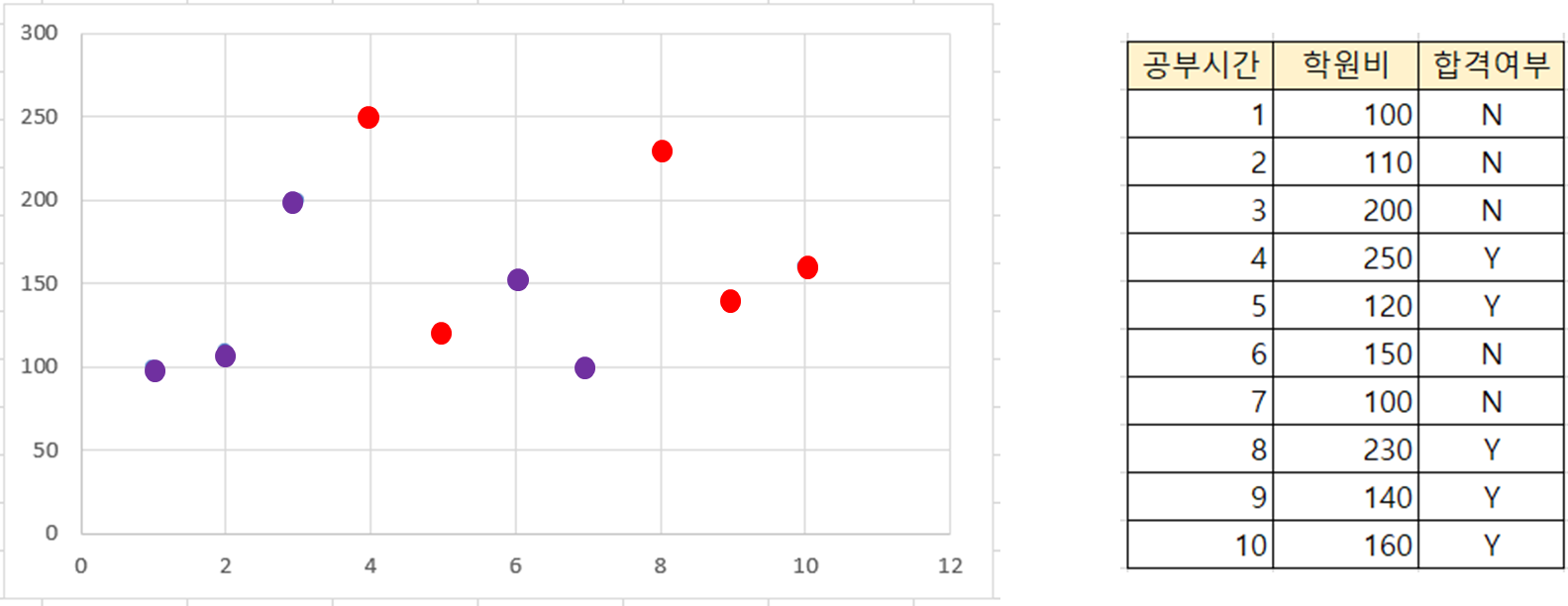
가능한 분기점에 대한 지니 불순도를 순차적으로 계산하여 비교한다.
공부시간을 기준으로 1과 2 사이의 1.5부터 9와 10 사이의 9.5까지 9개의 분기점을 살펴본다.
합격 데이터와 불합격 데이터가 각각 다섯 개씩 존재하므로 분기 전의 불순도는 0.5이다.
* 첫 번째 분기점 : (1 + 2) / 2 = 1.5


* 두 번째 분기점 : (2 + 3) / 2 = 2.5
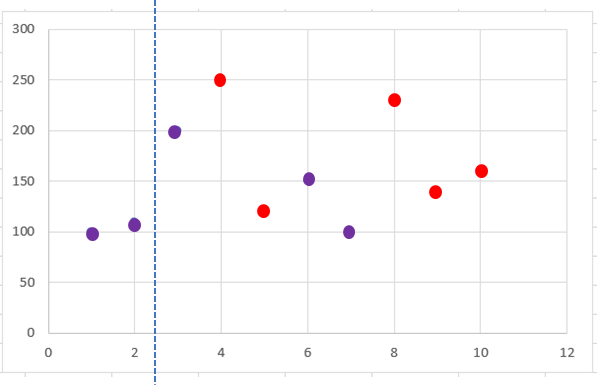
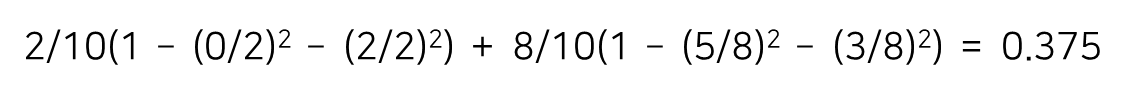
...
* 마지막 분기점 : (9 + 10) / 2 = 9.5
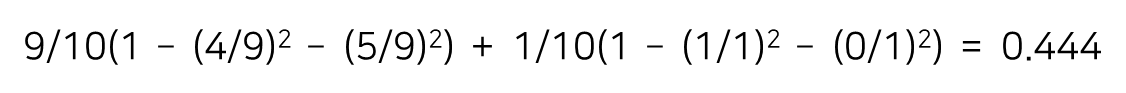
이번에는 학원비 변수를 분기의 기준으로 같은 과정을 수행한다.
순차적으로 분기점을 적용하기 편하도록 학원비를 기준으로 오름차순 정렬된 데이터를 활용한다.
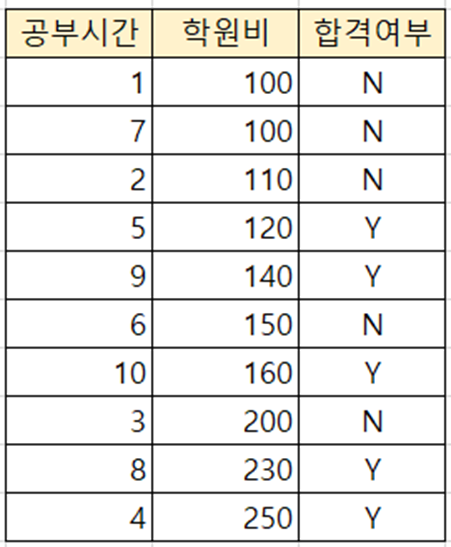
* 첫 번째 분기점 : (100 + 100) / 2 = 100


...
이처럼 공부시간과 학원비를 기준으로 가능한 모든 분기점의 지니 계수를 확인한 후,
불순도가 제일 낮은, 즉 제일 분류를 잘 할 것으로 판단되는 지점을 실제 분기점으로 사용한다.
예를 들어 공부시간 6을 기준으로 분할했을 때 지니 계수가 가장 낮았다면,
6시간을 기준으로 두 개의 서브셋이 생성되고 각 서브셋에서 다시 분기가 발생한다.
모든 노드의 불순도가 0이 될 때까지 이와 같은 과정을 반복하여 수행한다.
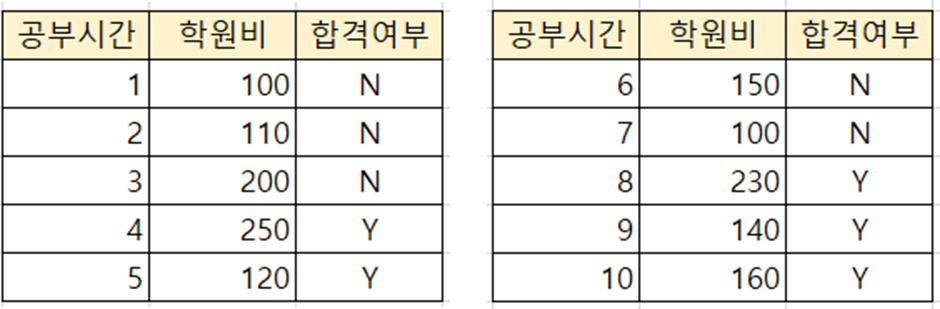
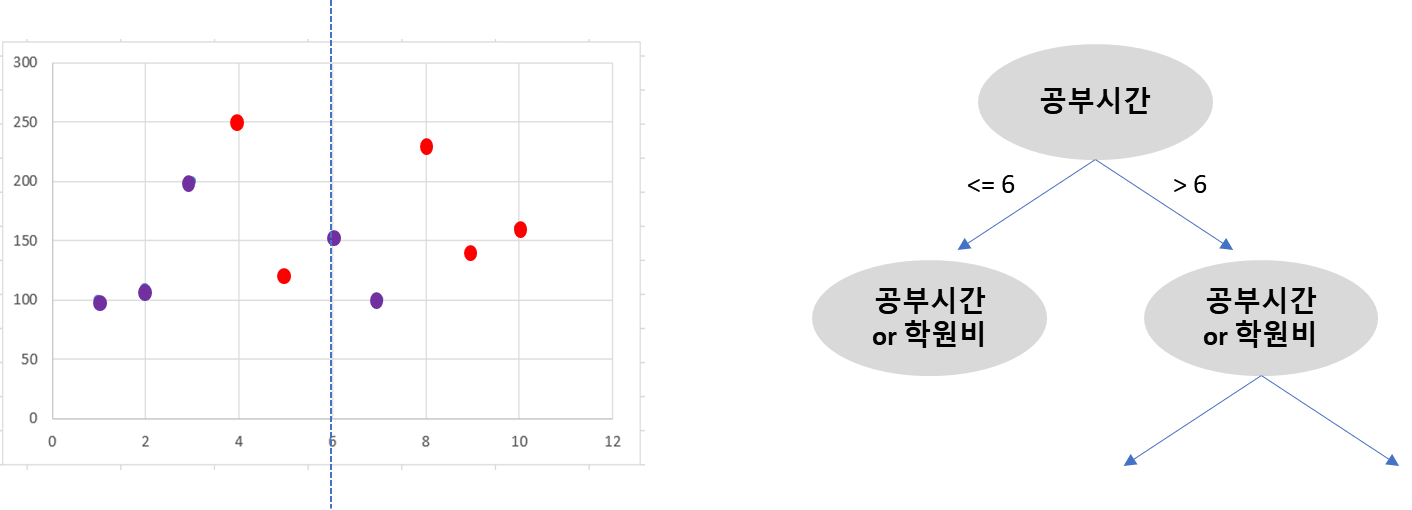
* 범주형 변수의 분기점
공부시간과 학원비는 수치형/연속형 변수에 해당한다.
기준변수가 범주형 변수라면 분기가 가능한 모든 경우의 수를 조사한다.
세 개의 범주 A, B, C가 존재하는 경우
- {A} vs. {B, C}
- {B} vs. {C, A}
- {C} vs. {A, B}
ex) 온도와 습도에 따른 외출 여부
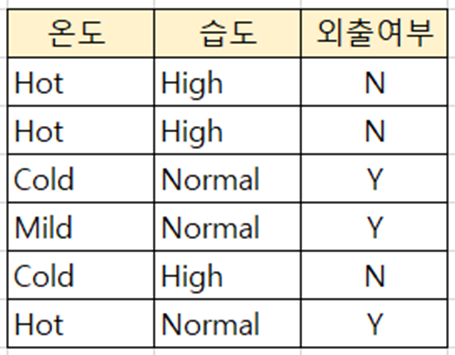
(1) 온도
- {Hot} vs. {Mild, Cold}
- {Mild} vs. {Cold, Hot}
- {Cold} vs. {Hot, Mild}
(2) 습도
- {High} vs. {Normal}
하이퍼 파라미터(Hyper Parameter) 튜닝
Decision Tree 모델에 투입되는 데이터가 복잡할수록 분기가 많이 발생하고 depth가 증가한다.
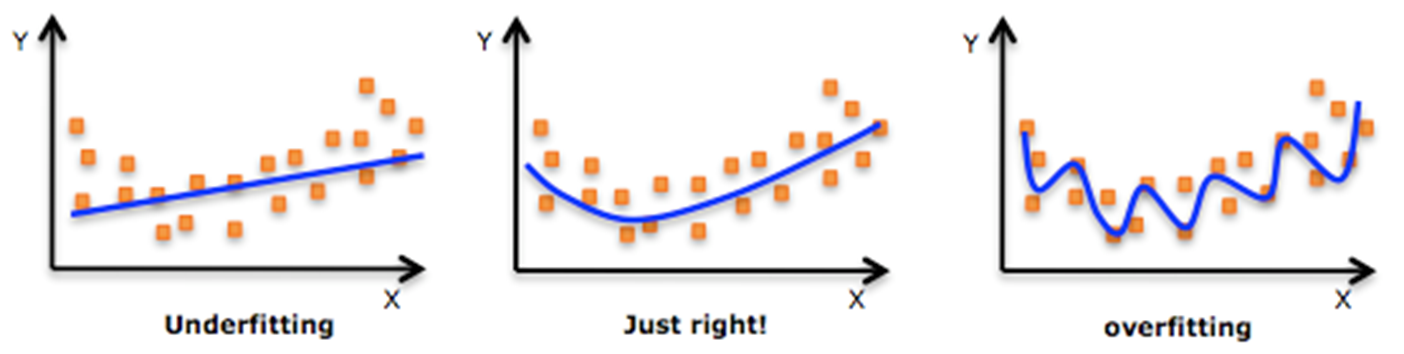
모든 노드의 불순도가 0이 될 때까지 depth를 증가시킬 경우 노드의 수가 지나치게 많아지면서
다소 쉽게 학습 데이터에 대한 과적합(Overfitting)이 발생할 수 있다.
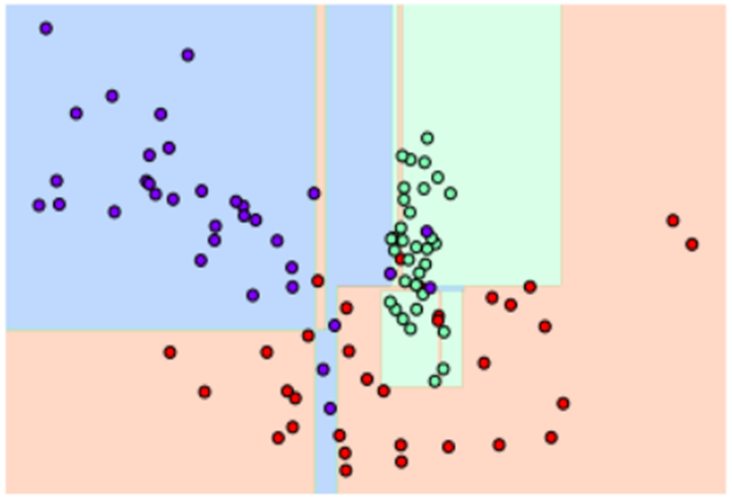
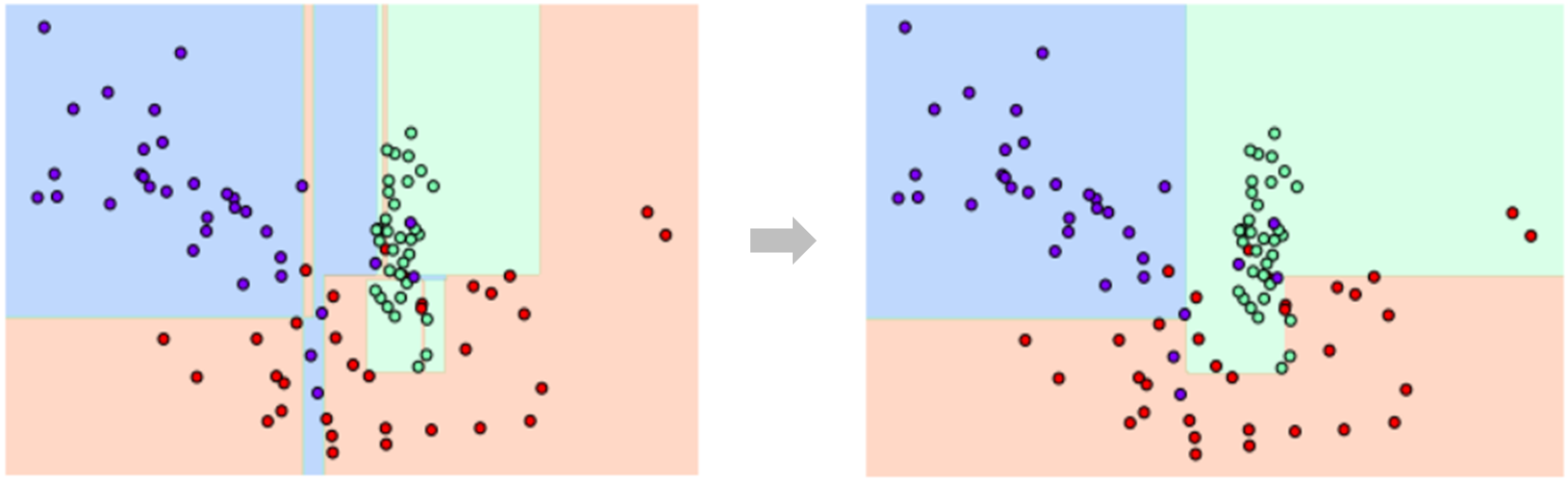
위 사례를 보면 이상치(Outlier)에 의해 여러 개의 무의미한 결정 경계가 생성되었다.
이러한 경우 모델의 복잡도가 증가하고 과적합으로 인한 성능 저하가 발생할 수 있다.
과적합이 쉽게 발생하는 Decision Tree 모델의 단점을 보완하고자 하이퍼 파라미터 튜닝을 한다.
조건을 만족하는 경우에만 경계면을 만들기 때문에 과적합을 방지할 수 있다.
- min_samples_split : 노드 분할에 필요한 최소 샘플 수(default: 2)
- min_samples_leaf : Leaf node가 되기 위해 필요한 최소 샘플 수(default: 1)
- max_features : 노드 분할에 사용할 최대 feature 개수
- max_depth : Decision Tree의 최대 깊이
- max_leaf_nodes : Leaf node의 최대 개수
실습에는 min_samples_leaf, max_depth 파라미터를 주로 사용할 예정이다.
max_features 파라미터는 잘 사용되지 않는 하이퍼 파라미터이다.
Decision Tree 모델 생성에는 sklearn.tree 모듈의 DecisionTreeClassifier API를 사용한다.
* Method
- fit(x, y) : 학습 데이터를 이용하여 모델 학습
- predict(x) : 모델에 테스트 데이터를 입력하여 계산된 예측값(y) 반환
- score(x, y) : 모델에 테스트 데이터를 입력하여 모델의 성능(정확도) 반환
* Attribute
- classes_ : 학습에 사용된 클래스의 label 정보
- feature_importances_ : 학습에 사용된 특성이 분류 결과에 영향을 미치는 정도
유방암 진단 데이터에 대한 Decision Tree 모델 실습 코드는 아래 링크에서 확인할 수 있다.
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-15-decision_tree.ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 17. 회귀 모델 성능 비교 (0) | 2022.07.05 |
|---|---|
| 16. 분류(3): Ensemble (0) | 2022.07.05 |
| 14. 분류(1): Logistic Regression (0) | 2022.06.29 |
| 13. Kaggle 프로젝트: 자전거 대여 수요 예측 (0) | 2022.06.29 |
| 12. 선형 회귀(2): 성능 평가 지표와 규제 선형 회귀 (0) | 2022.06.29 |