차원을 축소하여 복잡도를 줄이면서 정보의 손실을 최소화할 수 있는 방법
변수(feature) 간의 독립성이 만족되면 이론적으로는 변수가 많아질수록 모델의 성능이 향상된다.
하지만 실제로는 변수들이 독립적이지 않고, 변수의 수가 일정 수준 이상이 되면 성능이 저하된다.
머신러닝에서 차원(Dimension)은 변수(feature) 하나하나를 의미한다.
독립변수가 한 개면 1차원, 두 개면 2차원, ... , n개면 n차원인 식이다.
차원의 저주(Curse of Dimensionality)
앞서 말했듯이 변수의 수, 즉 차원이 증가하면 모델의 복잡도가 높아지고 성능이 저하된다.
이처럼 차원이 커지면서 한정된 관측치로 증가하는 차원의 패턴을 잘 설명하지 못하게 되고,
모델의 성능이 저하되는 현상을 차원의 저주(Curse of Dimensionality)라고 한다.
차원이 커지면 데이터 간의 거리가 증가하여 모델의 예측 신뢰도가 하락한다.
아래 그림에서 실데이터의 수는 다섯 개로 일정하지만, 차원의 수가 점점 늘어남에 따라
존재하는 데이터로 설명할 수 없는 빈 공간이 많아진다.

차원 축소(Dimension Reduction)
차원 축소는 고차원 학습 데이터를 저차원 데이터(3차원 이하)로 변환하여 학습시간을 절약하고,
시각적으로 보다 쉽게 데이터의 패턴을 인지할 수 있도록 하는 것을 말한다.
차원 축소 과정에서 정보의 손실을 최소화하고 데이터의 설명력을 높게 유지하는 것이 중요하다.
대표적인 차원 축소 기법으로 주성분 분석(PCA, Principal Component Analysis)이 있다.
규제 회귀 방식(Ridge, Lasso, ElasticNet)도 차원 축소법의 일종이다.
회귀 계수가 0에 가까운 컬럼을 삭제하는 Lasso 규제는 보다 직관적인 차원 축소 방식이다.
CNN(Convolutional Neural Network)은 인간의 시신경을 모방하여 만든 딥러닝 구조로,
이미지 분석 시 정보 소실을 최소화하기 위해 활용하는 차원 축소 기법이다.
딥러닝에 사용되는 기법이므로 참고만 하도록 한다.
차원 축소는 크게 두 가지 방식으로 이루어지는데,
각각 변수 선택(Feature Selection)과 변수 추출(Feature Extraction)이다.
주성분 분석(PCA)은 변수 추출 방식을 사용한다.
변수 선택(Feature Selection)
변수 선택은 데이터의 특징을 잘 나타내주는 변수(feature)만 선택하는 방식이다.
전처리 실습 과정에서 머신러닝에 필요 없는 feature를 drop한 것도 변수 선택에 해당한다.
최근에 등장한 머신러닝 모델(Boosting)의 경우 중요 변수를 추출하는 알고리즘이 내장되어 있어
다른 모델들에 비해 우수한 성능을 보인다.
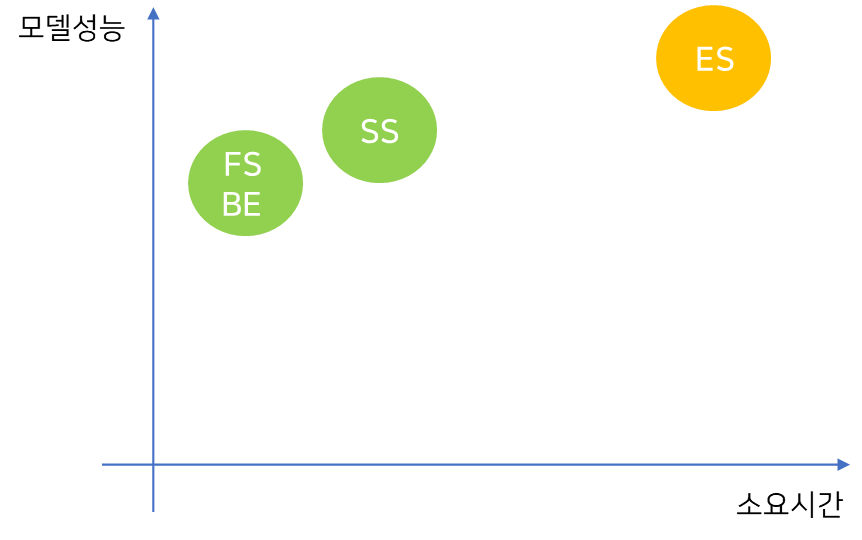
다음의 네 가지 변수 선택 방식이 존재한다.
- 전역 탐색(Exhausitve Search)
- 전진 선택(Forward Selection)
- 후진 제거(Back Elimination)
- 단계 선택(Stepwise Selection)
* 현실적으로 가능한 방식은 전진 선택, 후진 제거, 단계 선택의 세 가지 뿐이다.
(1) 전역 탐색(Exhaustive Search)
가능한 모든 경우를 시도하여 최적의 feature 조합을 찾는 방식으로,
할 수만 있다면 최고의 방법이지만 현실적으로 불가능하다. (2**p - 1가지 경우의 수 발생)

(2) 전진 선택(Forward Selection)
설명변수가 하나도 없는 상태에서 시작하여 유의미한 변수부터 차례로 모델에 추가하는 방식이다.

학습 데이터에 x1부터 x5까지 다섯 개의 변수가 존재한다고 할 때,
다음과 같이 변수를 하나씩 추가하면서 각 경우의 결정계수(R²)를 비교해 최적의 조합을 찾는다.
3단계에서 다른 변수를 추가해도 모델의 성능이 나아지지 않으므로 최적의 조합은 x3, x4이다.

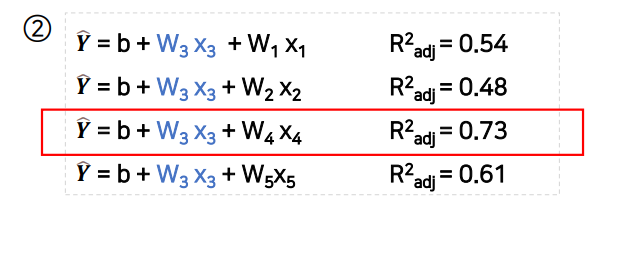
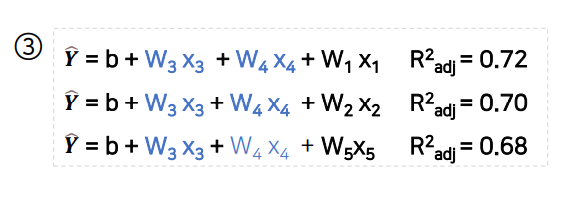
(3) 후진 제거(Back Elimination)
설명변수를 모두 포함한 상태에서 시작하여 가장 적은 영향을 주는 변수부터 제거하는 방식이다.
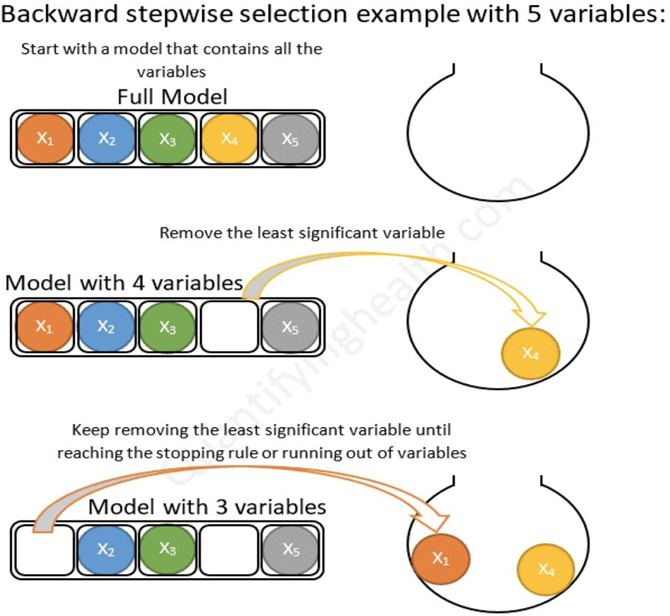
마찬가지로 x1부터 x5까지 다섯 개의 변수가 존재하는 경우,
이번에는 아래 상태에서 출발하여 추가로 변수를 제거하는 것이 성능 저하를 가져올 때 멈춘다.
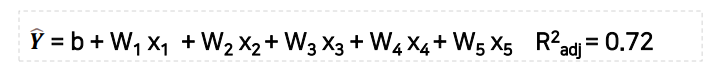
(4) 단계 선택(Stepwise Selection)
변수가 하나도 없는 상태에서 시작하여 전진 선택과 후진 제거를 번갈아가며 수행하는 방식이다.
이후 과정에서 한 번 선택된 변수가 제거되거나 제거된 변수가 재선택 될 수 있다.
전진 선택법과 후진 제거법에 비해 시간이 많이 소요되지만 좋은 성능을 보인다.
변수 추출(Feature Extraction)
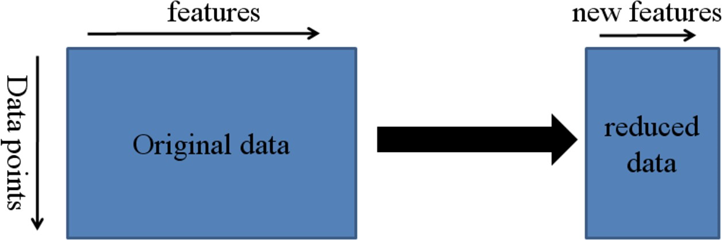
기존의 데이터를 주요 성분/feature를 포함한 저차원 데이터로 압축하여 추출하는 방식으로,
원본 데이터의 고차원 feature 공간을 저차원의 새로운 feature 공간으로 투영한다.
기존 feature를 조합하여 데이터를 잘 설명할 수 있는 새로운 feature를 추출해낸다.
변수 추출 모델은 내장된 알고리즘으로 높은 설명력의 상관관계를 가진 feature들을 찾아,
선별된 변수를 대상으로 분산 값을 구하는 등 모델 내부에서 추가적인 계산을 수행한다.
이 같은 방식으로 고차원 데이터의 변동을 최대한 보존하면서 저차원 데이터로 변환한다.
변수 추출 시 내부적인 계산을 통해 중요한 성분을 포함한 새로운 feature를 추출하기 때문에,
추출된 feature는 기존 데이터의 feature와 다른 값을 가지게 된다.
주성분 분석(PCA)이 대표적인 변수 추출 방식의 차원 축소 기법이다.
주성분 분석(PCA, Principal Component Analysis)
주성분 분석은 차원 축소를 위해 분포의 주성분을 분석하는 기법으로,
변수가 너무 많아 기존 feature를 조합한 새로운 변수로 모델을 생성할 때 사용된다.
(* 주성분: 전체 feature의 분산/변동을 가장 잘 설명하는 성분)
주성분 분석의 목적은 데이터를 충분히 잘 설명할 수 있는 새로운 축을 찾아내는 것이다.
예를 들어 x1, x2 두 개의 축을 가진 2차원 데이터를 1차원으로 축소하려고 한다.
가장 쉬운 방법은 둘 중 하나의 축으로 모든 데이터를 이동시키는 것이다.
하지만 그렇게 할 경우, 아래 그림의 x1, x2 축과 같이 겹치는 데이터 생겨 정보가 소실된다.
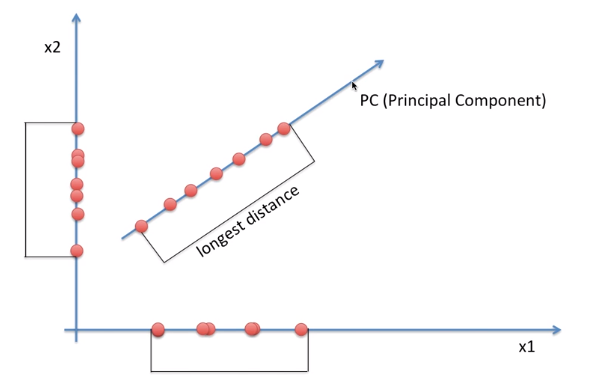
차원을 축소하면서 발생하는 정보의 유실을 최소화하기 위해서는 분산을 최대한 보존해야 한다.
분산이 커지면 점들 사이의 거리가 유지되어 데이터가 서로 겹치지 않고,
데이터가 겹치지 않으면 변수들 간의 차이가 명확하여 효율적인 분석이 가능하다.
다음은 데이터가 퍼져 있는 정도인 분산이 최대가 되는 축을 찾아나가는 과정이다.
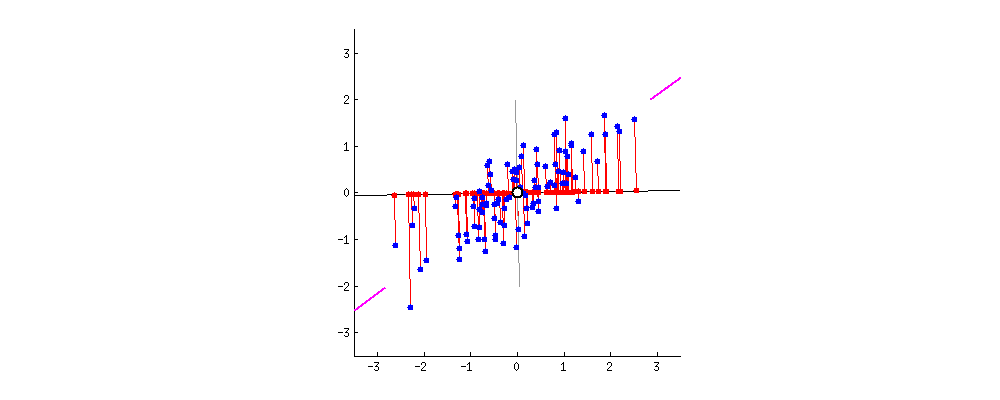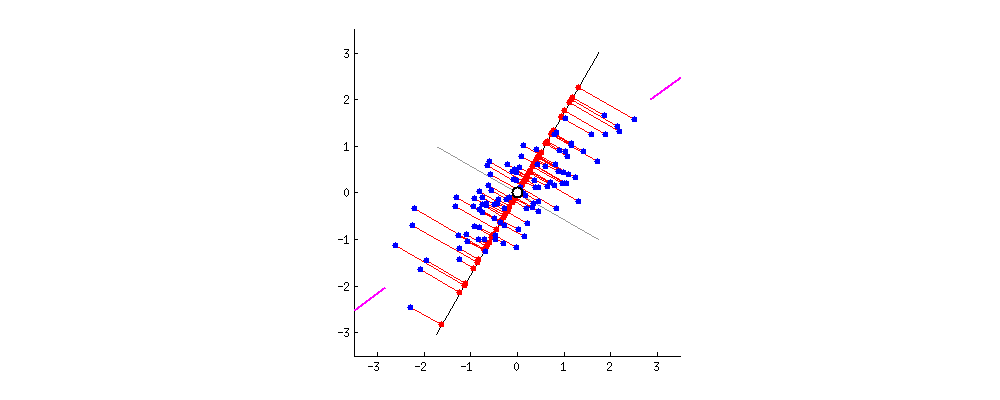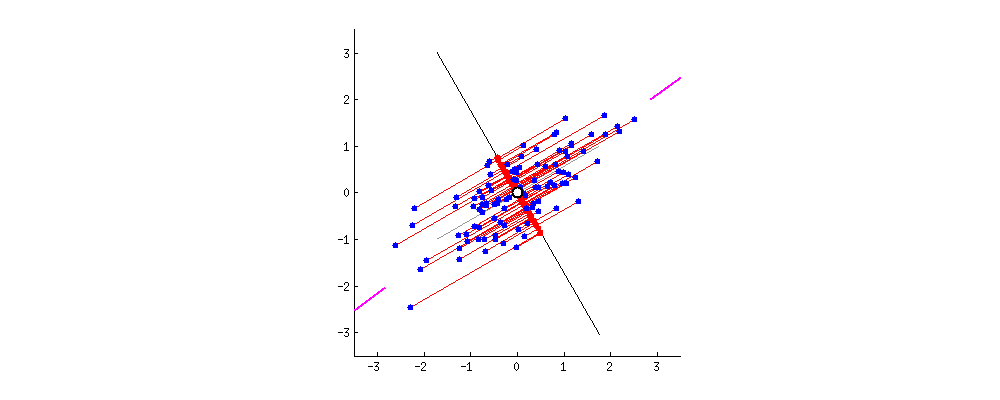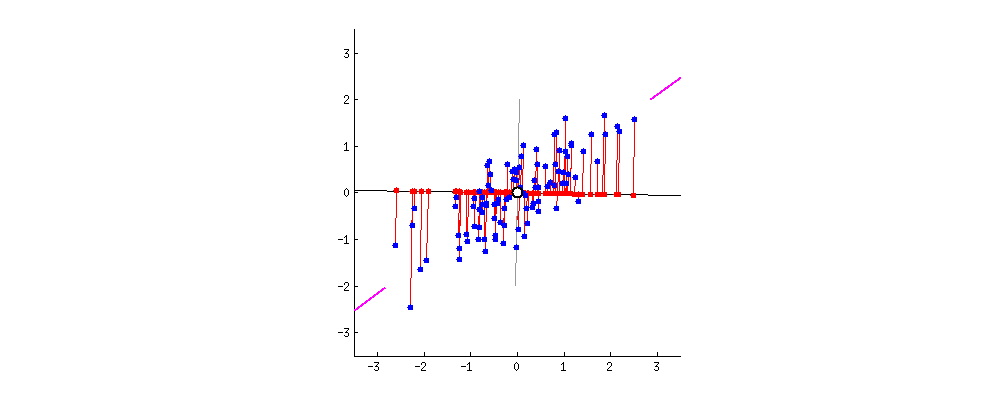
주성분 분석(PCA)에서는 학습 데이터의 분산이 최대인 축을 먼저 찾고,
이 첫 번째 축과 직교하면서 분산을 최대한 보존하는 두 번째 축을 찾는다.
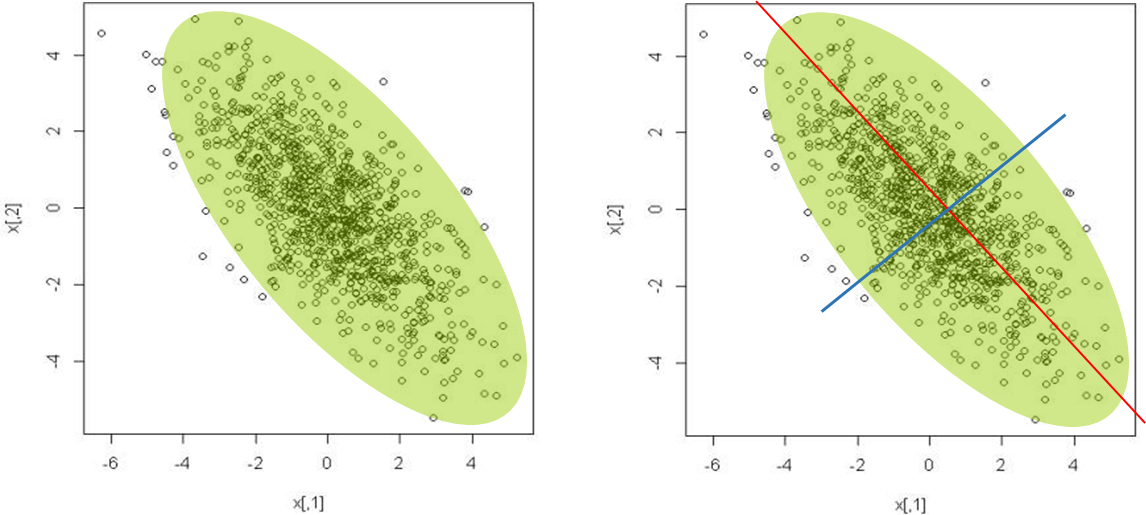
3차원 이상의 데이터라면 처음 두 개의 축에 직교하고 분산이 최대인 세 번째 축을 찾을 수 있다.
PCA 알고리즘은 데이터의 차원(feature)의 개수만큼 여러 방향의 직교하는 축을 찾는다.
이처럼 i번째 축을 정의하는 단위 벡터를 i번째 주성분(PC, Principal Component)이라고 한다.
축이 결정되면 모델 내부에서 축을 기준으로 데이터의 값을 변환하는 작업을 거친다.
PCA를 구현하기 위한 API는 sklearn.decomposition에 포함되어 있다.
* Argument
- n_components : PCA로 변환할 차원의 수
* Method
- fit_transform(x) : x에 차원 축소를 적용
- inverse_transform(x) : 데이터를 원래의 차원 공간으로 변환
* Attribute(적절한 차원의 수 결정에 사용)
- explained_variance_ : component 별 변동성(분산)
- explained_variance_ratio : component 별 변동성 비율
변동성 비율은 축소된 차원(축)이 원본 데이터의 변동성을 얼마나 반영하는지 나타내는 비율이다.
각 component가 전체 데이터에 대해 어느 정도의 설명력을 가지는지 알 수 있다.
차원 축소 시 적절한 차원의 수를 결정하는 데에 사용된다.
차원 축소와 주성분 분석을 완전히 이해하기 위해서는,
공분산 행렬과 고유값(eigenvalue) 등 수학적 지식이 뒷받침되어야 한다.
데이터 사이언스와 머신러닝을 깊이 있게 이해하기 위한 수학 공부의 필요성을 느낀다.
아래 링크에서 주성분 분석(PCA) 실습 코드를 확인할 수 있다.
https://github.com/tldnjs1231/data-analytics/blob/main/data-analytics-19-pca.ipynb
GitHub - tldnjs1231/data-analytics
Contribute to tldnjs1231/data-analytics development by creating an account on GitHub.
github.com
'2022 데이터 사이언스 > 빅데이터 분석과 모델링' 카테고리의 다른 글
| 20. 군집 분석: K-Means Clustering (0) | 2022.07.10 |
|---|---|
| 18. Kaggle 프로젝트: 호텔 예약 (0) | 2022.07.05 |
| 17. 회귀 모델 성능 비교 (0) | 2022.07.05 |
| 16. 분류(3): Ensemble (0) | 2022.07.05 |
| 15. 분류(2): Decision Tree (0) | 2022.07.05 |