Linear Combination is an important notion in linear algebra.
2-2. Linear Combinations
The goal is to understand,
- Linear combination and vector equation
- Span
- Existence of solutions in a linear system
- Matrix-matrix multiplication as linear combination of vectors
Linear Combinations
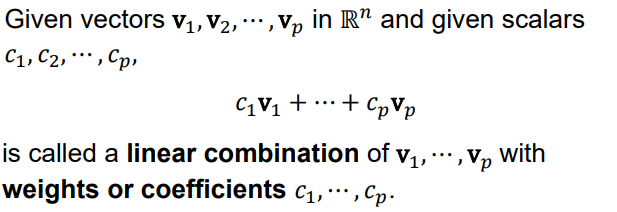
The weights in a linear combination can be any real numbers, including zero.
Some vectors with the weight of zero may not be used.
From Matrix Equation to Vector Equation
The life-span equation is currently expressed as a matrix-vector multiplication.

A matrix equation can be converted into a vector equation:

We can represent a set of linear equations into either a matrix form or a vector equation form.
Span
Now the issue is
1) how to solve the linear system in terms of a vector equation,
2) and sorting out the situation where the solution to Ax = b exists given our linear system in the form of vector equation.
We must first go over the notion of span.
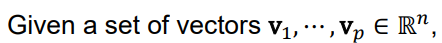
the span of these vectors Span {v1, ... , vp},
is defined as the set of all linear combinations of the given vectors v1, ... , vp.

Span {v1, ... , vp} is also called,
* Geometric Description of Span
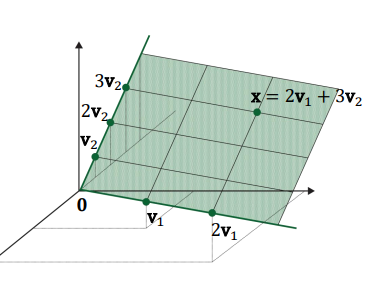
Given the two vectors v1 and v2 in the three-dimensional space above,
the span of these two vectors is basically all the points contained in this plane.
Following is a more formal description.
If v1 and v2 are


For example, 2v1 + 3v2 is one point on the plane.
Accumulating all these points, an infinitely stretching plane,
which is the span of the two vectors v1 and v2, will be formed.
Back to the life-span example,
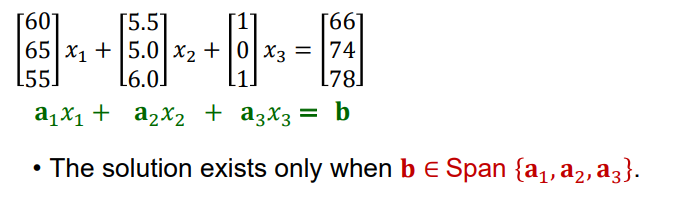
This is an important condition to guarantee a solution for our linear system.
Matrix Multiplications
There are some useful ways to understand matrix-matrix multiplications.
Matrix multiplications can be viewed as,
- Linear combinations of vectors
- Column combinations
- Row combinations
- Sum of rank-1 outer products
1) Matrix Multiplication as Linear Combinations of Vectors
Matrix-vector multiplication
→ Linear combination of the three columns in matrix A with coefficients in vector x
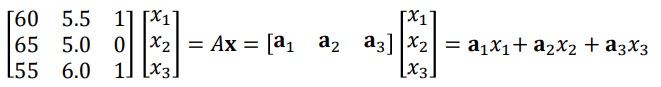
2) Matrix Multiplication as Column Combinations
Linear combinations of columns
→ Left matrix : bases, right matrix : coefficients
The left matrix provides its columns as ingredient vectors,
and each column of the right matrix works as a linear combination coefficient
to produce each of the columns in the resulting matrix.

3) Matrix Multiplication as Row Combinations
Linear combinations of rows of the right matrix
→ Right matrix : bases, left matrix : coefficients
The row vectors on the right provides a common ingredient vector set,
and each row of the left matrix works as a linear combination coefficient
to produce each row of the resulting matrix as x transpose and y transpose.

4) Matrix Multiplication as Sum of Rank-1 Outer Products

One thing to note here is that
regardless of whether u1, u2, v1, v2 are scalars or vectors,
we can simply treat them as scalars when performing inner product u1v1 and u2v2.
We will further talk about the rank of a matrix in the next post.
'2022 수학 & 통계학 > 데이터 사이언스를 위한 수학의 기초' 카테고리의 다른 글
| 04. Linear Algebra(3): Linear Independence (0) | 2022.06.08 |
|---|---|
| 02. Linear Algebra(1): Basic Elements of Linear Algebra (0) | 2022.06.08 |
| 01. Course Overview (0) | 2022.05.25 |