Data Science ← Machine Learning, Artificial Intelligence, Big Data
1-1 Brief Overview of Machine Learning
What is Machine Learning?
A subfield of Artificial Intelligence that gives computers the ability to learn without being explicitly programmed.
"Learning"
▶ Any process a system improves performance from experience
Application of Machine Learning
1) Systems that can automatically adapt and customize themselves to individual users (personalization)
2) Systems that are too difficult or expensive to construct manually
3) Discover new knowledge from a large dataset
4) Mimic human and replace certain autonomous tasks
Why Machine Learning?
- Increasing amount of available data
- Many basic effective and efficient algorithms (ex: R, Python)
* The data is abundant, but the knowledge is expensive and scarce.
Therefore, we use machine learning techniques to generate knowledge.
Categories of Machine Learning
1) Supervised Learning
Given examples of inputs(x1, x2) and desired outputs(O, X), which are labeled data,
predict outputs on future inputs, extract general rules.
ex) classification, regression, time series prediction
* We have training data with correct answers to prepare the algorithm

2) Unsupervised Learning
Given only inputs(unlabeled data), automatically discover hidden features.
ex) clustering, outlier detection
* Identification of natural groups in data
Throw data into the algorithm without training data,
hope it make some kind of sense out of the data.

3) Semi-supervised Learning
Given both labeled and unlabeled data, leverage information to improve both tasks.
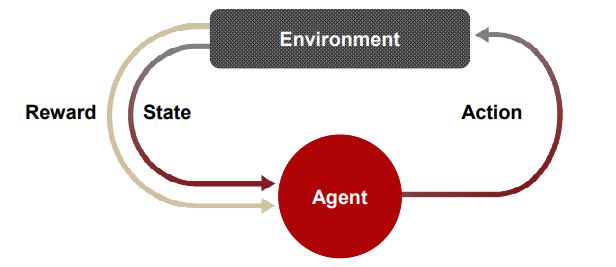
4) Reinforcement Learning
(1) the agent observes the state of the environment
(2) the agent performs tasks/actions based on the observation
(3) scalar rewards and punishments given from the environment
* Learn to select action sequences in a way that maximizes expected reward
Some Types of Machine Learning Algorithms
1) Regression(prediction)
Predicting a variable from data observations
2) Classification
- Assigning observations to predefined groups
- Predicting class from observations
3) Clustering
- Splitting observations into groups based on similarity
- Grouping observations into "meaningful" groups
4) Association
Seeing what often appears together with what
ex) people who buy diapers also tend to buy beer
Machine Learning and Other Disciplines
(1) Statistics
Inference from a sample
(2) Mathematics
Linear algebra and calculus to
- solve regression problems
- optimization functions
(3) Operations research or Computer science
Efficient algorithms to
- solve the optimization problem
- represent and evaluate the model of inference
* Basically, all mathematics
- Probability & Statistics
- Linear algebra
- Calculus & Optimization
- Graph theory
1-2 Introduction to Mathematical Fundamentals for Data Science
Machine Learning theory intersects statistical, probabilistic, computer science,
and algorithmic aspects.
Mathematical Fundamentals are necessary for a good understanding on
- how the machine learning algorithm works
- how we can get good results and interpret them properly
* This course will be focused on
1) Linear algebra, 2) Probability & statistics, 3) Multivariable calculus & optimization
Linear Algebra
Study of vectors and linear functions
"Vector"
▶ an object having both a magnitude and a direction
We use the arrow to represent a vector(a)

- -a : a vector with the same magnitude as a but is pointed in the opposite direction
- λa : pointing the same direction as the direction of a, λ times the magnitude of a
Addition of Vectors
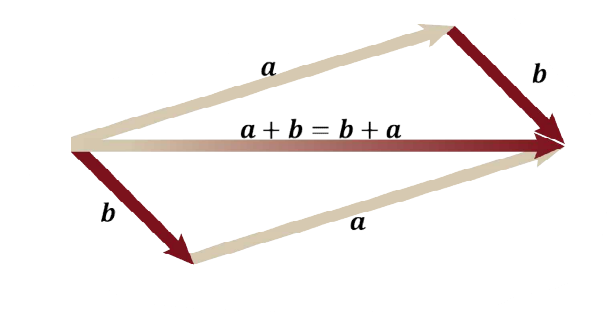
* Things covered in this course
- Operations on or between vectors and matrices
- Span, linear independence, basis, dimension, ...
- Linear transformations
- Least squares problem
Probability & Statistics
Uncertainty is the key concept in Machine Learning
Probability theory is the mathematical study of uncertainty.
The design of machine learning algorithms often relies on probabilistic assumption of the data.
* Things covered in this course
- Random variables, probability distribution, expectation, variance
- Common distributions : Bernoulli, Binomial, Geometric, Poisson, Exponential, Uniform, Gaussian distributions
- Joint and conditional distribution, independency, joint Gaussian
- Basic statistics, confidence interval, hypothesis test, t-test
Optimization
Helps finding models to explain the data, fit machine learning models on the data
by choosing the parameters that either maximize or minimize a function.
ex) likelihood of the data, loss function, error obtained by the model on the (training) data
* Things covered in this course
- Introduction to mathematical programming modeling
- Linear programming and duality
- Basics of multivariable calculus : derivatives, gradient, Hessian
- Convex set and function
- Nonlinear programming, Lagrangian relaxation and KKT conditions
- Numerical optimization algorithms : gradient and Newton's algorithms
Basic Mathematical Concepts & Notations
1) Set Theory
Collection of objects which are called elements of the set
ex)
N = {1, 2, -4, 5}, M = {man, woman}
- ℝ : set of real numbers
- ℤ : set of integers
- ∅ : empty set
- |N| : cardinality(size) of a set N, number of elements in N
- A⊆B : subset, every element in A is also an element of B
- A⊂B : proper subset, A⊆B and A≠B
- A∩B : intersection, set of elements which both sets have in common
- A∪B : union, set of elements which belong to at least one of the sets
- A×B : Cartesian product, {(a, b) | a ∈ A and b ∈ B}
ex) A×B = {(a, c), (a, e), (c, c), (c, e)} when A = {a, c}, B = {c, e}
Specification of sets
- List notation : {a, c, d, f}, {-1, 1, 3, 5, 7}, ...
- Predicate notation : stating properties of its elements, {x | x ∈ ℤ and x < 7}, ...
- Recursive rules : defining a set of rules which generates its members
ex) (a) 2 ∈ A, (b) if x ∈ A, then x + 3 ∈ A, (c) nothing else belongs to A
A = {2, 5, 8, ... }
2) p-Norms
The norms are normally used to calculate a length or a magnitude of a vector or matrices.
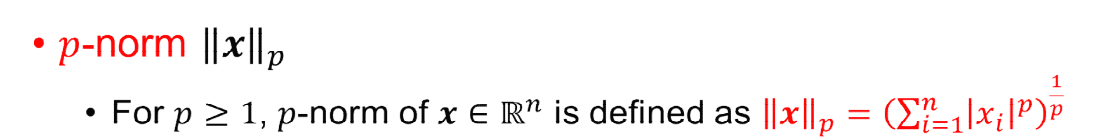
The following are three types of norms that are frequently encountered.

- 1-norm : the sum of the absolute values of all the elements in x
- 2-norm : the square root of the sum of the squares of the elements
* also called the Euclidean norm
: the 2-norm normally represents the Euclidean distance.
- infinity-norm : the maximum absolute value entry in x
Some Basic Notations
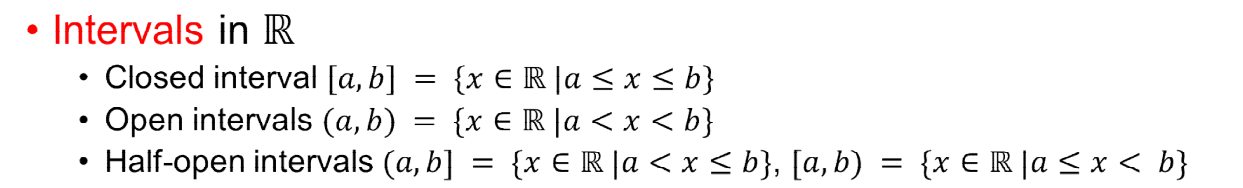
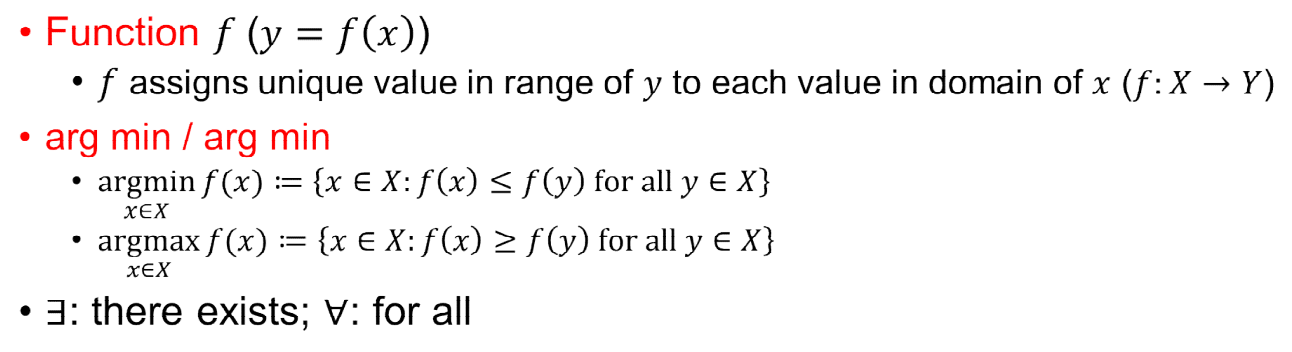
(1) arg min : argument of the minimum
The arg min of f(x) over the set X
- the set of x's such that f(x) is less than or equal to f(y) for all y's in the set X
- a collection of x's which induce the minimum value of function f
(2) arg max : argument of the maximum
The arg max of f(x) over the set X
- the set of x's for which function f attains its largest value
'2022 수학 & 통계학 > 데이터 사이언스를 위한 수학의 기초' 카테고리의 다른 글
| 04. Linear Algebra(3): Linear Independence (0) | 2022.06.08 |
|---|---|
| 03. Linear Algebra(2): Linear Combinations (0) | 2022.06.08 |
| 02. Linear Algebra(1): Basic Elements of Linear Algebra (0) | 2022.06.08 |